Esercizi di Logica
Esercizio 1
Descrivere il sistema formale per l'alfa-equivalenza
Esercizio 2
Fornire una derivazione (nello stile della Def.2.3 di [SM])
della formula ben formata (\x.xy)(zz)=alfa(\w.wy)(zz)
nel sistema formale per l'alfa-equivalenza a partire dall'insieme vuoto.
Esercizio 3
Fornire le definizioni di regola ammissibile e derivabile.
Dimostrare che nel sistema formale della alfa-equivalenza
la seguente regola e' derivabile
M =alfa N M' =alfa N' M" =alfa N"
------------------------------------------
M"MM' =alfa N"NN'
Esercizio 4
Convincersi che le dimostrazioni delle proposizioni da 3.2 a 3.12
del testo [SM] dimostrano veramente quello che devono dimostrare.
Esercizio 5
Considerare le seguenti formule ben formate e dire se
sono soddisfacibili, contraddittorie o tautologie.
not(p -> p)
p -> (p -> q)
(p -> p) -> not(p)
((p -> q) -> q) -> q
not(q -> not(q -> p))
(p -> r) -> ((q -> r) -> ((not(p)->q) -> r))
Dire se e' vero che
p -> (p -> q) |= p -> q
not(p -> p) |= (p -> q) -> (q -> p)
p -> (p -> q), not(p -> p) |= (p -> q) -> (q -> p)
Esercizio 6
Dimostrare che tutti gli assiomi del calcolo proposizionale
sono tautologie.
Dimostrare che se le ipotesi della regola di inferenza del modus ponens sono
tautologie, allora la conclusione e' una tautologia.
Esercizio 7
Giustificare il fatto che
dimostrare
A,B |= C
e' equivalente a dimostrare che
not(A->not(B))->C
e' una tautologia
Esercizio 8
Dimostrare che, nel calcolo proposizionale, una regola di inferenza
A1 A2 ... An
----------------
C
e' ammissibile se e solo se
( |= A1, |= A2 .... e |= An) implica |= C
Utilizzare questa proprieta' per dimostrare quindi che la regola
not(A -> not(B))
---------------------
A
e' ammissibile.
Soluzione. (by luca98, josura e gabriele7)
Esercizio 9
Si prendano in considerazione le definizioni per le formule
A /\ B
A \/ B
A <-> B
date alla fine del secondo punto della Definizione 3.1 in [SM]
(dove /\ si legge "and", \/ si legge "or" e <-> si legge "equivalente a",
oppure "se e solo se" oppure "doppia implicazione" ecc. )
Dimostrare che, dato un assegnamento proposizionale,
- la formula A /\ B e' vera (il suo valore di verita' e' 1) se e solo se
A e' vera e B e' vera
- la formula A \/ B e' falsa (il suo valore di verita' e' 0) se e solo se
A e' falsa e B e' falsa
- la formula A <-> B e' vera (il suo valore di verita' e' 1) se e solo se
A e B hanno lo stesso valore di verita' (cioe' entrambe 1 o entrambe 0).
Esercizio 10
DImostrare le proposizioni da 3.2 a 3.12
del testo [SM] utilizzando la deduzione naturale.
Esercizio 11
Considerare la deduzione naturale con le solo regole
per l'implicazione, la negazione e l'assurdo.
Dimostrare che, definendo \/ e /\ come fatto alla fine del
secondo punto nella definizione 3.1 [SM], tutte le regole
della deduzione naturale per \/ e /\ sono derivabili o ammissibili.
Esercizio 12
Nella logica dei predicati, considerare la segnatura seguente, dove
i simboli di funzione sono
{c0, k0, f1, g2}
mentre i simboli di predicato (relazioni) sono
{P1, Q2}
Fornire delle strutture (non banali) nelle quali le seguenti formule
risultino vere e strutture nelle quali risultino false.
forall x.Q(x,x)
forall x. forall y.Q(x,y)
forall x. forall y. exists z. (P(x) -> Q(y,f(z)))
exists z. forall x. (P(x) \/ Q(k,z))
exists z. (P(g(z,c)) /\ (forall x. Q(x,f(g(z,k)))))
Esercizio 13
Considerare la segnatura dell'esercizio 12 e scrivere
una grammatica di Chomsky che generi il linguaggio di
tutte le formule ben formate di tale segnatura.
Dire di che tipo e' la grammatica fornita.
Esercizio 14
Fare qualche esercizio tra quelli proposti in [AU].
Esercizio 15
Consideriamo la segnatura che non abbia alcun simbolo di funzione
e che abbia i seguenti simboli di predicato (relazione): {P,Q}, dove P e' binario
e Q e' ternario.
Si consideri la struttura che ha come supporto l'insieme dei numeri naturali
ed in cui P corrisponda alla relazione "≤" tra naturali e Q corrisponda alla
seguente relazione ternaria tra numeri naturali: {(n,m,p) | n+m=p}.
Quali delle seguenti formule sono vere nella struttura data?
forall x. forall y. forall z.(Q(x,y,z) -> Q(y,x,z))
forall x. exists y. (Q(x,x,y) -> Q(y,x,y))
exists x. exists y. (P(x,y) \/ not(B(y,x,y)))
(forall x. exists y. P(x,y)) -> forall x. Q(x,x,c)
exists x. forall y. Q(x,y,x)
forall x. forall y. P(x,y)
exists x. exists y. P(x,y)
(forall x. exists y. not(P(x,y)) -> exists y. not(P(y,c)
Esercizio 16
Stabilire quali delle formule seguenti sono valide e quali
soddisfacibili. Nel secondo caso, fornire un esempio di struttura
che non ne e' un modello (in cui cioe' non siano vere).
(exists x.A(x) -> forall x.B(x)) -> forall x.(A(x) -> B(x))
(exists x.A(x) -> exists x.B(x)) -> forall x.(A(x) -> B(x))
(exists x.A(x) -> exists x.B(x)) -> exists x.(A(x) -> B(x))
(exists x.((A(x) -> B(x)))) -> (forall x.A(x) -> forall x. B(x))
(exists x.((A(x) -> B(x)))) -> (forall x.A(x) -> exists x. B(x))
(exists x.((A(x) -> B(x)))) -> (exists x.A(x) -> exists x. B(x))
(forall x.((A(x) -> B(x)))) -> (exists x.A(x) -> forall x. B(x))
(forall x.((A(x) -> B(x)))) -> (exists x.A(x) -> exists x. B(x))
(forall x.((A(x) -> B(x)))) -> (forall x.A(x) -> forall x. B(x))
(forall x.A(x) -> forall x. B(x)) -> (forall x.((A(x) -> B(x))))
(forall x.A(x) -> exists x. B(x)) -> (exists x.((A(x) -> B(x))))
(forall x.A(x) -> exists x. B(x)) -> (forall x.((A(x) -> B(x))))
Esercizio 17
Sia data la seguente formula della logica dei predicati con uguaglianza:
forall p. forall q.((P(p,a)/\not(p=a)) -> exists x. exists y.(f(x,y)=f(q,q)/\g(x,y)=p))
Stabilire se e' soddisfatta nelle seguenti interpretazioni:
- Il supporto sono i numeri naturali dispari, 'a' corrisponde a 19, 'f' alla funzione esponente, 'g' al prodotto e P alla relazione '≤'.
- Il supporto sono i numeri naturali, 'a' corrisponde a 1, 'f' alla funzione somma, 'g' al prodotto e P alla relazione '≤'.
- Il supporto sono i numeri reali, 'a' corrisponde a 0, 'f' alla funzione somma, 'g' al prodotto e P alla relazione '≥'.
Esercizio 18
Dimostrare che il supporto di strutture che sono domini di PA
contiene almeno un sottoinsieme numerabile di elementi.
Dimostrare nell'Aritmetica di Peano che 2+1=3.
Esercizio 19
(a)
Fornire la definizione di sistema formale e di regola di inferenza ammissibile.
(b)
Cosa significa, nel calcolo proposizionale (logica proposizionale),
che una formula A e' conseguenza tautologica di un insieme di formule
Gamma ( Gamma |= A) ?
E' vera la seguente affermazione?
p -> (p -> q) |= p -> q
dove p e q sono variabili proposizionali.
(c)
Consideriamo la segnatura che non abbia alcun simbolo di funzione
e che abbia i seguenti simboli di predicato (relazione): {P,Q}, dove P e' binario
e Q e' ternario.
Si consideri la struttura che ha come supporto l'insieme dei numeri naturali
ed in cui P corrisponda alla relazione "≤" tra naturali e Q corrisponda alla
seguente relazione ternaria tra numeri naturali: {(n,m,p) | n+m=p}.
Quali delle seguenti formule sono vere nella struttura data?
forall x. forall y. forall z.(Q(x,y,z) -> Q(y,x,z))
(forall x. exists y. P(x,y)) -> forall x. Q(x,x,c)
Soluzione.
Esercizio 20
(a)
Cos'e un sistema formale? Cos'e' un sistema formale alla Hilbert per la logica?
Cos'e' un sistema formale di deduzione naturale per la logica?
(b)
Dimostrare in deduzione naturale che A → B, A → C ⊢ A → ((B/\C) \/ D)
(c)
Dimostrare il teorema di deduzione di Herbrand per la logica proposizionale.
Ricordiamo che gli assiomi per la logica proposizionale sono:
- α → (β → α)
- α → (β → γ) → ((α → β) → (α → γ))
- (not β → not α) → ((not β → α) → β)
Soluzione.
Esercizio 21
Cos'e' un sistema formale? Quando un sistema formale si dice Consistente?
Quando un insieme di formule ben formate di un sistema formale e' una Teoria?
Cos'e' la Teoria pura di un sistema formale? Una teoria pura e' una teoria? Perche'?
Esercizio 22
Quella che segue e' una dimostrazione, nella logica dei predicati,
di α, ¬α ⊢ β . A tale dimostrazione pero'
mancano delle parti.
1. α → (¬β → α) Ak
2. ?? ipotesi
3. ¬β → α MP(1,??)
4. ¬α → (¬β → ¬α) Ak
5. ¬α ipotesi
6. ?? MP(4,5)
7. (¬β → ¬α) → ((¬β → α) → β) A¬
8. ?? MP(6,7)
9. β ??
Completare la dimostrazione riempiendo le parti "??".
Soluzione.
Esercizio 23 NO a.a.17/18
Descrivere i principi di Induzione, Induzione completa ed Induzione Ben Fondata
ed un loro possibile uso nell'Informatica.
Esercizio 24
Sia {{a,b},{c2,p2}} una segnatura dove a e b sono simboli di costante, mentre c e p
sono simboli predicativi binari.
Interpretando a come "Antonella", b come
"Bruno", c(x, y) come "x conosce y", p(x, y) come "x e' parente di y",
traducete le seguenti frasi (scrivete cioe' le formule ben formate corrispondenti):
(i) Bruno ha un parente che conosce qualcuno;
(ii) un parente di Bruno conosce tutti quelli che non sono conosciuti da Antonella;
(iii) se un parente di Antonella conosce Bruno, Bruno conosce tutti quelli che conoscono Antonella.
Soluzione.
Esercizio 24.1
Sia {{},{c1, g1, p2, a2}} una segnatura dove c e g sono simboli
predicativi unari, mentre p e a
sono simboli predicativi binari.
Interpretando
c(x) come "x e' un cane", g(x) come "x e' un gatto",
p(x,y) come "x e' il padrone di y" e
a(x,y) come "x ama y"
traducete le seguenti frasi (scrivete cioe' le formule ben formate corrispondenti,
avendo a disposizione entrambi i quantificatori e tutti i connettivi logici):
(i) ogni cane non ama alcun gatto;
(ii) tutti i cani e i gatti hanno un padrone;
Scrivere inoltre la frase in italiano corrispondente alla seguente formula ben formata:
∀x.((c(x) ∧ ¬∃y.p(y,x)) → ∀z.¬a(z,x))
Soluzione.
Esercizio 25
Sia α una formula ben formata della logica dei predicati del prim'ordine
(calcolo dei predicati) rispetto una data segnatura Σ e sia
AΣ una struttura.
Dare le definizioni di:
- α e' soddisfacibile in AΣ
- α e' vera in AΣ
- α e' soddisfacibile
- α e' valida (o vera)
- α e' contraddittoria
Esercizio 26
Consideriamo la segnatura Σ={{},{r2}}.
Sia α la formula ben formata ∀x. ∃y. (r(x, y) ∧ ¬r(y, x)) .
(i) Dimostrate che non esiste una struttura AΣ
tale che il supporto di AΣ sia l'insieme {0,1}
e tale che α sia vera in AΣ
(ii) Costruite un'interpretazione AΣ
tale che α sia vera in AΣ
Soluzione.
Esercizio 27
Dimostrare in deduzione naturale la proposizione 3.10 del testo di Martini,
cioe' che α → β ⊢ ¬β → ¬α
Soluzione.
Esercizio 27.1
Dimostrare che in deduzione naturale la regola
¬¬α
-------
α
e' derivabile.
Fare lo stesso per la regola
α
-------
¬¬α
Soluzione.
Esercizio 27.2
Dimostrare che gli assiomi del sistema per il calcolo
proposizionale descritti nel testo di Martini sono
teoremi nel sistema di deduzione naturale.
Soluzione.
Esercizio 28
Definendo la congiunzione (∧) in termini di implicazione
e negazione (come indicato nel Martini), dimostrare che
la regola di inferenza (∧ E), cioe'
α ∧ β
--------
α
e' derivabile nel sistema di deduzione naturale
senza le regole per (∧) e (∨)
Soluzione.
Esercizio 29
Definendo la congiunzione (∧) in termini di implicazione
e negazione (come indicato nel Martini), dimostrare che
la regola di inferenza (∧ I), cioe'
α β
------------
α ∧ β
e' derivabile nel sistema di deduzione naturale
senza le regole per (∧) e (∨)
Soluzione.
Esercizio 30
Dimostrare, nel sistema di deduzione naturale per la logica proposizionale
che
(A∨B)→(A∧B) ⊢ A→B
Soluzione.
Esercizio 31 NO a.a.17/18
Dimostrare nel sistema a' la Hilbert della logica dei predicati
(quello del testo [SM]) che nell'Aritmetica di Peano 1+2=3.
Cioe' che
PA ⊢ S(0)+S(S(0))=S(S(S(0)))
Soluzione. (by G.Valenti)
Esercizio 31.1
Dimostrare nel sistema di deduzione naturale che nell'Aritmetica di Peano 1+2=3.
Cioe' che
PA ⊢ S(0)+S(S(0))=S(S(S(0)))
Esercizio 32 NO a.a.17/18
Si consideri la seguente definizione di funzione Haskell dai naturali agli interi:
f 100 = 0
f n = if n > 100 then n + (f 0) else (f (n+1)) - 1
Dimostrare che f e' totale e che coincide con la funzione intera g(x) = x - 100.
Aiutino Utilizzare l'induzione ben-fondata sull'insieme ben-fondato
(N,[), dove N e' l'insieme dei numeri naturali e
la relazione di precedenza [ e' definita come segue:
n [ m sse (n=0 e m >100) oppure (m<100 e n=m+1)
Soluzione. (by F. Brischetto)
Esercizio 33 NO a.a.17/18
Si consideri la seguente funzione Haskell dai naturali ai naturali:
f 0 = 5
f 1 = 8
f 2 = 11
f n = 9 + f (n-3)
Dire perche' non si puo' dimostrare che il calcolo di (f n) termina
per ogni naturale n utilizzando l'induzione ben fondata sull'insieme
ben fondato (N,[), dove la relazione di precedenza [ e' definita come segue:
n [ m sse (n e' diverso da 0,1,2 e n≥m), oppure (n e' uguale a 0,1 o 2 e m=3).
Esercizio 34 NO a.a.17/18
Modificare la definizione della relazione [ dell'esercizio 33, in modo
che (N,[) sia ben fondato e si riesca a dimostrare per induzione ben fondata
che il calcolo di (f n) termina per ogni n. Dimostrare, sempre per induzione
ben fondata, che il valore di (f n) coincide, per ogni n, con 3n+5.
Esercizio 35
Sia D un sistema formale.
Dimostrare che una regola
α1 ... αn
(R) ---------------------
β
e' ammissibile in D se e solo se:
⊢ D α1, ..., ⊢ D αn
implica
⊢ D β
Esercizio 35.2
Si consideri il sistema formale D per l'α conversione nel λ-calcolo
e si consideri la seguente regola di inferenza R1:
x =α y
(R1) --------------------
xλz.z =α yλv.v
R1 e' derivabile in D?
E' ammissibile in D?
Giustificare le risposte.
Si consideri ora la regola
λx.x = α λx.λy.x
(R2) --------------------
x =α y
R2 e' derivabile in D?
E' ammissibile in D?
Giustificare le risposte.
Esercizio 35.3
Si consideri il sistema formale D i cui giudizi sono stringhe sull'alfabeto {a,b}.
D ha un solo assioma:
(Ax) ------------
aaa
ed una sola regola di inferenza:
w
(R) ------------
waa
dove w puo' essere qualsiasi sequenza formata da sole a.
Si consideri ora la seguente regola:
b
(R') ------------
baa
R' e' derivabile in in D?
E' ammissibile in D?
Giustificare le risposte.
Soluzione. (by josura)
Esercizio 35.4
Il sistema formale dell'esercizio 35.3 e' consistente?
Giustificare adeguatamente la risposta.
Esercizio 36
Descrivere il sistema formale del Calcolo Proposizionale (Logica Proposizionale)
e descrivere brevemente come si puo dimostrare nel Calcolo proposizionale che
Γ ⊢ α, dove α e'una fbf e Γ un insieme di fbf.
Soluzione.
Esercizio 37
Descrivere, nel linguaggio dell'aritmetica di Peano,
le formule ben formate P(x) e Q(x,y,z) corrispondenti, rispettivamente,
alle seguenti relazioni sui numeri naturali:
- x e' un numero dispari
- z e' il minimo comune multiplo di x e y
Sia R la seconda relazione. E' vera la seguente affermazione?
(n,m,p)∈R se e solo se PA ⊢ Q(n,m,p)
Perche?
Soluzione.
Esercizio 38
Fornire una prova in deduzione naturale
a cui sia possibile associare il lambda-termine
che codifica il numerale di Church 2
Soluzione.
Esercizio 39
Cosa e' una Segnatura Σ per la logica dei predicati del prim'ordine
(calcolo dei predicati)? Fornire la definizione di struttura
AΣ per una segnatura Σ.
Esercizio 40
Dimostrare in deduzione naturale che
¬ A → ¬B ⊢ B → A
e che ¬(A → B) ⊢ ¬ B
Dimostrare una delle due cose utilizzando il teorema di correttezza e completezza.
Soluzione.
Esercizio 41 NO a.a.17/18
Cosa si intende con numero di Goedel di una formula di PA?
Enunciare alcuni risultati limitativi della logica.
Esercizio 42
Enunciare e discutere brevemente del I Teorema di Incompletezza di Goedel.
Soluzione.
Esercizio 43
Sia {{a0,b0},{c2,p2}} una segnatura dove a e b sono simboli di costante, mentre c e p
sono simboli predicativi binari.
Interpretando a come "Antonella", b come
"Bruno", c(x, y) come "x conosce y", p(x, y) come "x e' parente di y",
traducete le seguenti frasi (scrivete cioe' le formule ben formate corrispondenti):
(i) Ogni parente di Bruno ha un parente che conosce Bruno;
(ii) Un parente di Bruno conosce una persona che conosce tutti i parenti di Antonella;
(iii) Se Antonella e Bruno hanno un parente in comune, allora sono parenti.
Soluzione.
Esercizio 44 NO a.a.17/18
Si consideri la seguente definizione di funzione Haskell dai naturali agli interi:
f 100 = 0
f n = if n > 100 then n + (f 0) else (f (n+1)) - 1
Dimostrare che f e' totale e che coincide con la funzione intera g(x) = x - 100.
Aiutino Utilizzare l'induzione ben-fondata sull'insieme ben-fondato
(N,[ ), dove N e' l'insieme dei numeri naturali e
la relazione di precedenza [ e' definita come segue:
n [ m sse (n=0 e m >100) oppure (m<100 e n=m+1)
Soluzione.
Esercizio 45
Nella seguente deduzione per
¬α → α ⊢ P0 α
scrivere cosa va inserito al posto di '??' e correggere i due errori presenti,
giustificando le correzioni fatte.
1. (¬α → ¬α) → ((¬α → α) → α) A¬
2. ¬α → ¬α Proposizione 3.1
3. (¬α → α) → α ??
4. ¬α → α ipotesi
5. ¬α ipotesi
Dimostrare ¬α → α ⊢ α
anche nel sistema di deduzione naturale.
Soluzione.
Esercizio 46
Quelli seguenti sono tre dei teoremi che state studiando (avete studiato) nel corso
di Elementi di Analisi:
Teorema di esistenza ed unicita' della radice n-esima aritmetica.
Siano a un numero reale non negativo e n un numero naturale.
Allora esiste uno ed un solo numero reale non negativo b tale che
b alla n e' uguale ad a
Teorema di esistenza ed unicita' del logaritmo.
Siano a e b due numeri reali positivi, con a diverso da 1.
Allora esiste uno ed un solo numero reale x tale che a alla x e' uguale a b
Proprieta' caratteristiche dell'estremo superiore.
Sia A un sottoinsieme di R, non vuoto e limitato superiormente.
Un numero reale r e' l'estremo superiore di A se e solo se verifica le seguenti
proprieta':
i) x minore o uguale ad r per ogni x in A
ii) per ogni epsilon maggiore di zero, esiste un elemento x in A tale che x e' maggiore
di r meno epsilon.
Specificare una segnatura (con meno simboli possibile) ed utilizzarla
per fornire le formule ben formate corrispondenti a questi teoremi.
Soluzione.
Esercizio 46
Dimostrare in deduzione deduzione naturale per la logica del primo ordine che, nella teoria dei gruppi (vedi [AAb]),
l'elemento neutro e' unico.
(Ricordarsi che nella logica del primo ordine:
∃v.A equivale a ¬ ∀v.¬A
A→B equivale a ¬A ∨ B
A ∨ B equivale a ¬(¬A ∧ ¬B)
¬¬A equivale ad A)
Soluzione.
Esercizio 47
Si consideri la seguente deduzione:
[¬p(z)]1 q(s) ∀x.∀y.((¬p(x) ∧ q(y)) → ¬r(y,x))
------------------------- --------------------------------------
¬p(z) ∧ q(s) (¬p(z) ∧ q(s)) → ¬r(s,z)
-----------------------------------------------------------------
∃x.¬p(x) ¬r(s,z) ∀x.∀y.r(y,x)
---------------------------------------------------------------- (1) ----------------------
¬r(s,z) r(s,z)
---------------------------------------------------------------------------------------------------
⊥
Si indichino i nomi delle regole utilizzate.
Una delle regole e' utilizzata in modo scorretto. Indicare la regola ed il motivo per cui
e' utilizzata scorrettamente.
Soluzione.
Esercizio 48
Se si utilizza un sistema (come quello utilizzato in [SM]) dove il quantificatore esistenziale
e' definito in termini di quello universale,
mostrare che
∃x.∃y.¬r(y,x)
e' equivalente a ¬∀x.∀y.r(y,x).
Dimostrare che
∃x.∃y.¬r(y,x)
e' equivalente a ¬∀x.∀y.r(y,x).
nel caso di utilizzi un sistema che contiene esplicitamente sia la quantificazione esistenziale
che quella universale (come in [AU]),
ed in cui la funzione di interpretazione, su una struttura AΣ,
della fbf ∃x.α, rispetto ad un ambiente ρ, e' definita da
[[∃x.α]]ρ = 1 sse esiste un elemento a nel supporto di AΣ
tale che [[α]]ρxa = 1
Esercizio 49
Dimostrare che se nel sistema di deduzione naturale la regola
(∃-E) viene utilizzata senza alcuna condizione, allora
sarebbe possibile dimostrare ∃x.α → ∀x.α.
Soluzione.
Esercizio 50
Descrivere il sistema formale del Calcolo dei Predicati (Logica dei Predicati del primo ordine).
Esercizio 51
Dare la definizione di Teoria e di Teoria Pura.
Dimostrare che una Teoria Pura e' una Teoria.
Soluzione.
Esercizio 52
Dimostrare che la formula ben formata
(∀ x.∃ y. ¬P(x,y) ) → ∃ y. ¬P(y,c)
dove c e' una costante,
non e' un teorema della Logica dei Predicati del primo ordine.
Soluzione.
Esercizio 53
Descrivere il sistema formale del Calcolo dei Predicati
(Logica dei Predicati del primo ordine) nella sua versione
alla Hilbert o in deduzione naturale.
Esercizio 54 NO a.a.17/18
Scrivere, nel linguaggio dell'Aritmetica di Peano,
la formula ben formata P(x,y,z) corrispondente alla seguente
relazione sui naturali:
x e' un multiplo del quoziente della divisione di y e z
Dire inoltre se
e' vera la seguente affermazione:
(n,m,p)∈R se e solo se PA|- P(n,m,p)
Perche?
(ricordiamo che, se q e' un numero naturale, q e'il termine
che lo rappresenta
nel linguaggio di PA)
Soluzione.
Esercizio 55
Ricopiare la seguente dimostrazione (in deduzione naturale per la
logica proposizionale con operatori →, ¬, ∨ e ⊥) di
D, D→A, B→ (¬D ∨ C), A → (B∨C) |-- C
riempiendo le parti mancanti (indicate con sequenze di '?').
Indicare inoltre le regole nelle quali vengono scaricate le ipotesi (e quali
sono le ipotesi scaricate) e il nome delle regole utilizzate nella
deduzione.
???? D
-----------
???? ?? ???????? [B] ⊥
------------ -------------------------- ---------
????? A (¬D)∨C C ???
---------------------------- -------------------------------------------------
B∨C ?? [C]
------------------------------------------------------------------------------------
??
Soluzione.
Esercizio 56 NO a.a.17/18
Si forniscano le definizioni di Induzione, Induzione Completa ed Induzione Ben Fondata.
Si accenni poi alla corrispondenza tra Induzione e Ricorsione.
Esercizio 57
Data una segnatura Σ per la logica dei predicati del primo ordine,
definire l'insieme dei termini sulla segnatura Σ (TermΣ) e
l'insieme delle formule ben formate (FbfΣ).
Data inoltre una struttura AΣ ed una formula ben formata α
in FbfΣ, si dica quando α e' soddisfacibile in AΣ, α e' vera in AΣ (valida in AΣ),
α e' valida (o vera), α e' contradittoria.
Esercizio 58
Sia {{I0, F0}, {f1, s2, a2} } una segnatura dove 'I' e 'F' sono simboli di costante, 'f'
e' un simbolo di relazione unario, e 's' e 'a' sono simboli di relazione binari.
Interpretando I e F come "Italia" e "Francia", f(x) come "x e' un film", s(x, y) come "x e' uno spettatore del paese y", a (x, y) come "x ama y", si traducano le seguenti frasi (si scrivano cioe' le formule ben formate corrispondenti):
- ogni film non e' amato da uno spettatore italiano o francese;
- nessuno spettatore francese ama tutti i film;
- qualche spettatore italiano ama solo film che la Francia non ama.
Soluzione.
Esercizio 59
La seguente e' una deduzione incompleta in deduzione naturale per la seguente proposizione:
(A → B) → (¬¬A → ¬¬B).
[A]1 [ ]4
----------------
[ ]2 B
-----------------------
--------- [1]
[¬¬A]3
-------------------
⊥
------- [2]
----------- [3]
¬¬A → ¬¬B
--------------------- [ ]
(A → B) → (¬¬A → ¬¬B)
Ricopiare e completare la deduzione.
Soluzione.
Esercizio 60
Nella logica dei predicati del primo ordine (calcolo dei predicati),
si specifichi una segnatura Σ, una struttura AΣ e le due formule ben formate
vere in AΣ, corrispondenti alle due seguenti affermazioni:
- Il quadrato di un numero naturale maggiore di due e' maggiore del suo doppio
- Alcuni parenti di Carlo sono anche parenti di Bruno, ma non di Alberto
Soluzione.
Esercizio 61
Quella che segue e' una dimostrazione incompleta, in logica proposizionale (calcolo proposizionale),
di P, che utilizza l'ipotesi ¬¬P ed il teorema, che supponiamo gia' dimostrato, ¬P→¬P.
Ricopiare e completare tale dimostrazione.
1. ............. (Ak)
2. ............. ipotesi
3. ............. MP(1,2)
4. ............. (A¬)
5. ............. MP(3,4)
6. ¬P→¬P teorema
7. ............. MP(5,6)
Ricordiamo che gli assiomi (Ak) e (A¬)sono:
(Ak) α → (β→α)
(A¬) (¬β →¬α)→((¬β →α) →β)
Soluzione.
Esercizio 62
Fornire la definizione precisa di Sistema Formale. Elencare i nomi di almeno quattro sistemi formali.
Esercizio 63
Nella logica dei predicati del primo ordine (calcolo dei predicati),
si specifichi una segnatura Σ, una struttura AΣ e la formula ben formata
vera in AΣ, corrispondente alla seguente affermazione:
Tutti i conoscenti comuni a Mario e ad Antonio sono italiani, ma Mario ha anche conoscenti francesi.
Soluzione.
Esercizio 64
Si prendano in considerazione le seguenti definizioni (testo Martini):
A ∨ B = ((¬A) → B)
A ∧ B = ¬(¬A ∨ ¬B)
Dimostrare che, dato un assegnamento proposizionale,
- la formula A ∧ B e' vera (il suo valore di verita' e' 1) se e solo se A e' vera e B e' vera
- la formula A ∨ B e' falsa (il suo valore di verita' e' 0) se e solo se A e' falsa e B e' falsa
Soluzione.
Esercizio 65
Si consideri la seguente formula della logica dei predicati del prim'ordine su una segnatura
che contenga i simboli di predicato unari A e B:
(∃x.A(x)→∃x.B(x)) →(∃x.A(x)∧B(x))
Dimostrare che tale formula non e' valida.
Soluzione.
Esercizio 66
Nella logica dei predicati del primo ordine (calcolo dei predicati),
si specifichi una segnatura Σ, una struttura AΣ e la formula ben formata
vere in AΣ, corrispondente alla seguente affermazione:
Tutti i conoscenti comuni a Mario e ad Antonio sono italiani, ma Mario ha anche conoscenti francesi.
Soluzione.
Esercizio 67
Si consideri la logica dei predicati in deduzione naturale con uguaglianza.
Fornire una dimostrazione di
pippo=giuseppe |- ∀ x.(cugino(x,pippo) → cugino(x,giuseppe))
Ricordiamo che le due regole
per l'uguaglianza in deduzione naturale che sono utili per la dimostrazione sono le seguenti:
-------
x = x
x1 = y1 ... xn = yn
-------------------------------------------------
A[x/z] → A[y/z]
Dove A e' un qualsiasi simbolo di predicato n-ario. Inoltre con la notazione x
indichiamo una sequenza x1....xn di variabili.
Soluzione.
Esercizio 68
Sia {{},{s1, p1, a2}} una segnatura dove s e p sono simboli
predicativi unari, mentre a
un simbolo predicativo binario.
Interpretando
s(x) come "x e' uno studente", p(x) come "x e' un professore",
a(x,y) come "x apprezza y"
tradurre la seguente frase (scrivete cioe' la formula ben formata corrispondente,
avendo a disposizione entrambi i quantificatori e tutti i connettivi logici):
Alcuni studenti apprezzano tutti i professori, altri no.
Soluzione.
Esercizio 69
Dimostrare che
(∀ x.∃ y. ¬ P(x,y)) → (∃ y. ¬ P(y,c))
dove c e' una costante,
non e' derivabile nella logica del prim'ordine.
Soluzione.
Esercizio 70
Nel contesto della Logica Proposizionale (Calcolo Proposizionale),
fornire le definizioni di
- assegnamento proposizionale
- tautologia
- fbf (formula ben formata) soddisfacibile
- fbf contraddittoria
Esercizio 71
Ricopiare la seguente deduzione sostituendo correttamente i "???"
[A]1 [A→B]3
--------------------------- (→E)
??? [¬B]2
------------------------------------------------- (¬E)
???
----- (¬I)1
???
----------------- (→I)2
???
------------------------ (???)3
(A→B) → ((¬B)→¬A)
Soluzione.
Esercizio 72
Nel contesto della Logica Proposizionale,
dire, fornendone giustificazione, se la seguente affermazione e' corretta o meno:
Se Γ⊬ α allora Γ ⊢ ¬α
Soluzione.
Esercizio 73 NO a.a.17/18
Descrivere i principi di Induzione sui naturali, di Induzione Completa e di Induzione Ben-Fondata.
Esercizio 74
In quale punto della dimostrazione del Lemma di Deduzione di Herbrand viene utilizzata l'Induzione, e come?
Esercizio 75
Si consideri il seguente automa.
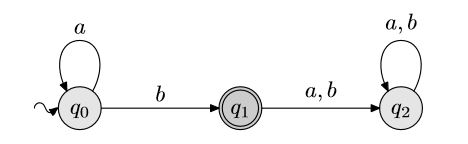
e il seguente linguaggio {an b | n≥0}.
Supponiamo di aver gia' dimostrato che le stringhe
della forma anb sono
riconosciute dall'automa.
Completare la dimostrazione che il linguaggio {an b | n≥0} coincide con il linguaggio
riconosciuto dall'automa, dimostrando formalmente per induzione che
le stringhe riconosciute dall'automa sono della forma anb.
Utilizzare il concetto di funzione di transizione δ e di
funzione
δ.
Si consideri che la funzione δ
puo' essere definita anche nel seguente modo:
δ(q,ε) = q
δ(q,ax) = δ(δ(q,a),x)
Soluzione.
Esercizio 76
Si fornisca la definizione di formula ben formata valida nella logica del primo ordine.
Si dimostri che la seguente formula, su una segnatura
che contenga i simboli di predicato unari A e B, non e' valida:
(∃x.A(x)→∃x.B(x)) →(∃x.A(x)∧B(x))
Possibile soluzione.
Esercizio 77
Si consideri il linguaggio con uguaglianza su una segnatura che abbia
{00, succ1,+2, ∗2} come simboli di funzione.
Supponendo che questi simboli di funzione siano interpretati col loro significato standard sul dominio
dei numeri naturali, si fornisca una formula ben formata che abbia z ed y come variabili libere e che
esprima la seguente frase
"z e' dispari e minore di y"
(si osservi che < non fa parte del linguaggio).
Soluzione.
Esercizio 78
Dimostrare nella logica dei predicati, nel sistema di deduzione naturale, che
(∀x. (A→B)) → ( (∀x.A) → (∀y.B))
Soluzione.
Esercizio 79
Fornire le definizioni, nella logica proposizionale (calcolo proposizionale), di tautologia
e conseguenza tautologica.
Accennare brevemente a come
si puo' decidere se una formula e' una tautologia o meno.
Esercizio 80
Fornire una deduzione nella logica proposizionale in deduzione naturale
per il teorema
((A∧B) → C)) → (A → (B → C))
Soluzione.
Esercizio 81
Dimostrare il seguente teorema della logica proposizionale:
Se Γ∪{α} e' contraddittorio, allora Γ |- ¬ α
Soluzione.
Esercizio 82
Si definisca il sistema formale della Logica Proposizionale (Calcolo Proposizionale) con
implicazione e negazione, nella versione alla Hilbert e in quella in Deduzione Naturale.
(b) La seguente deduzione contiene un errore. Individuarlo, giustificando la risposta.
[A]3 [¬A]1
-------------- ¬E
⊥
-------- ¬I(1)
¬¬A [¬A]1
----------------------------------- ¬E
⊥
------- ⊥
B
----------- →I(3)
A → B
Soluzione.
Esercizio 83
Si inserisca al posto di "??" una deduzione di |-- A → (B →) A e si fornisca la
forma normale del lambda
termine corrispondente alla deduzione risultante.
"??" A
--------------------------- →E
B → A B
-------------------------- →E
A
Soluzione.
Esercizio 84
Fornire la definizione di sistema formale e fornire un esempio di sistema formale.
Esercizio 85
Nella deduzione naturale per la logica proposizionale, fornire la dimostrazione del
seguente teorema
(A --> (B --> C)) --> ((A ∧ B) --> C))
Soluzione.
Esercizio 86
In deduzione naturale, dimostrare che, nel caso in cui x ∉FV(β)
|-- (∀x.(α → β)) → ((∃x. α)→ β)
Specificare in quale punto della deduzione fornita risulti indispensabile
l'utilizzo della condizione x ∉FV(β)
Soluzione.
Esercizio 87
Nel contesto della Logica del Primo Ordine (Calcolo dei Predicati),
fornire le definizioni di Segnatura, Termine e Formula Ben Formata (fbf).
Esercizio 88
Siano P e Q simboli di predicato unari.
Dimostrare in deduzione naturale il teorema
∀x.(P(x)→Q(x)) → (∀x.P(x)→∀x.Q(x))
Si dimostri inoltre che
∀x.(P(x)→Q(x)) → (∀x.P(x)→∀x.Q(x))
non e' un teorema.
Soluzione.
Esercizio 89 NO a.a.17/18
Enunciare e commentare brevemente il II Teorema
di Incompletezza di Goedel
Esercizio 90
Data una funzione di transizione δ di un automa a stati finiti,
definire la funzione
δ
e dimostrare formalmente che,
preso uno stato q e due stringhe x ed y,
δ(q,xy) = δ(δ(q,x), y)
Soluzione.
Esercizio 91 NO a.a.17/18
Fornire la definizione di Clausola di Horn.
Da cosa e' composto un programma Prolog?
Su quale proprieta' logica e' basato il funzionamento di Prolog?
Esercizio 92
Sia {{v0,prezzo1},
{prodottoInVendita1, scontato1, alcolico1, maggiore2}} .
una segnatura per la logica del primo ordine.
Interpretando
v come il numero 20, ed interpretando il simbolo di funzione prezzo ed i simboli di predicato
prodottoInVendita1, scontato1, alcolico1 e maggiore2
con il rispettivo senso che hanno in italiano,
tradurre la seguente frase (scrivete cioe' la formula ben formata corrispondente,
avendo a disposizione entrambi i quantificatori e tutti i connettivi logici):
Soluzione.
Esercizio 93
Dimostrare che non puo' esistere una derivazione per
∀y.(A(x) ∧ B(y)) |- ∀y.A(y) ∧∀y.B(y)
Soluzione.
Esercizio 94 NO a.a.17/18
Definire i principi di Induzione, Induzione completa e Induzione ben fondata.
Esercizio 95
Dimostrare in deduzione naturale il seguente teorema
((A ∧ B) ∧ C) → (A ∧(B ∧ C))
Soluzione.
Esercizio 96 NO a.a.17/18
Descrivere la relazione tra Induzione e Ricorsione.
Esercizio 97
Si consideri la seguente segnatura per la logica dei predicati con uguaglianza
(e con tutti i quantificatori e connettivi logici):
{{z0, exp2},{Nat1, <2}}.
Si consideri inoltre la struttura che abbia
come supporto i numeri reali ed in cui il simbolo di funzione z venga interpretato con il numero 0,
exp
con la funzione
di elevamento a potenza, il predicato Nat con il predicato
essere un numero naturale e il predicato < con minore stretto.
Si fornisca la formula ben formata la cui
interpretazione in tale struttura corrisponda alla seguente affermazione.
Siano a un numero reale non negativo e n un numero naturale.
Allora esiste uno ed un solo numero reale non negativo b tale che
b alla n e' uguale ad a
Soluzione.
Esercizio 98
Fornire in deduzione naturale una derivazione per
∀x.(A(x)→B(x)), ∃x.¬B(x) |- ∃x.¬A(x)
Soluzione.
Esercizio 99
Data una segnatura Σ per la logica dei predicati, definire cosa e'
una struttura AΣ per Σ.
Esercizio 100
Si dimostri che la fbf (ksk)(kkk)= sk e' un teorema del
sistema formale CL (sezione 2.2 di [SM]).
Soluzione.
Esercizio 101
Si supponga di aggiungere la seguente regola (cong) al sistema formale CL (sezione 2.2 di [SM])
M=N P=Q
-----------
MP=NQ
e si dimostri la fbf (ksk)(kkk)= sk utilizzando la regola (cong)
Soluzione.
Esercizio 102
Si supponga di aggiungere la seguente regola (cong) al sistema formale CL (sezione 2.2 di [SM])
M=N P=Q
-----------
MP=NQ
e si chiami CL' il sistema formale cosi' ottenuto.
Dimostrare che l'insieme dei teoremi di CL e quello dei teoremi di CL' sono identici.
Soluzione.
Esercizio 103
La seguente e' una dimostrazione non completamente specificata,
nel sistema formale CL, di
{k=sk} |-CL P=Q
Ricopiarla inserendo le parti mancanti.
1. ?? (ipotesi)
2. ?? (assioma refl)
3. kP = skP (cong2)(1.2.)
4. kPQ = kPQ (assioma refl)
5. kPQ = skPQ (congr)(3.4.)
6. ?? (Axk)
7. ?? (symm) (5.)
8. skPQ = P ??
9. skPQ = kQ(PQ) (Axs)
10. kQ(PQ) = Q (Axk)
11. skPQ = Q (trans)(9.10.)
12. P = skPQ ??
13. ?? ??
dove gli assiomi e regole di CL sono:
-------(axk) -------------(axs)
kMN=M sMNR=MR(NR)
R=R' RM=RN M=N M=N N=R
---------------(cong2) -----(symm) ---------(trans) ------(refl)
RM=R'N N=M M=R M=M
Quale proprieta' dell'insieme {k=sk} abbiamo dimostrato in questo modo?
Soluzione.
Esercizio 104
Nella logica proposizionale (calcolo proposizionale), cos'e' un assegnamento proposizionale?
Dato un assegnamento proposizionale B, definire la funzione
B e la nozione di tautologia.
Esercizio 105
Dimostrare in deduzione naturale che
A→C, B→C |- (A∨B)→C
Soluzione.
Esercizio 106
Sia {{},{scontato1, pv1, alcoolico1, costapiu1}}
una segnatura per la logica del primo ordine (calcolo dei predicati).
Si consideri la struttura che ha come supporto l'insieme di tutti i prodotti ed in cui
si interpreta
- scontato(x) come "x e' scontato";
- pv(x) come "x e' un prodotto in vendita";
- alcoolico(x) come "x e' alcoolico";
- costapiu(x) come "x costa piu' di venti euro".
Scrivere la fbf il cui valore di verita'
in tale struttura
coincide con quello della seguente frase in italiano
:
Tra i prodotti in vendita sono scontati
tutti e soli quelli che costano pi di
venti euro e non sono alcoolici
(Si hanno a disposizione entrambi i quantificatori e tutti i connettivi logici)
Soluzione.
Esercizio 107
Dimostrare che , se x non appartiene alle variabili libere di B,
allora
((∃x.A) → B) → ∀x.(A → B)
e' un teorema della logica dei predicati del primo ordine.
Soluzione.
Esercizio 108
Sia CL1
il sistema formale CL (vedi testo Martini [SM] pag. 7) in cui, al posto delle regole (CONGR1) e (CONGR2)
ci sia la seguente regola:
M=N P=Q
------------------------ (CONGR)
MP= NQ
DImostrare che sia (CONGR1) che (CONGR2) sono derivabili in CL1.
Soluzione. (by giorgio_buzzanca)
Esercizio 109
Fornire la definizione di sistema formale consistente.
Dato un sistema formale D ed un
insieme M di fbf, cosa significa che M e' una teoria in D? Cos'e' la teoria pura di D?
Esercizio 110
Dimostrare nel sistema di deduzione naturale per la logica del primo ordine che
∀ x.(A(x) → B(x)) ⊢ ¬ ( A(c) ∧ ¬B(c) )
dove c e' un simbolo di costante della segnatura.
Se nella deduzione proposta si utilizzano regole di inferenza che hanno vincoli di applicabilita',
descrivere tali vincoli e indicare perche' sono soddisfatti.
Soluzione.
Esercizio 111
Sia
{{M0,A0,I0, F0},
{persona1, conoscente2, cittadino1} }
una segnatura per la logica del primo ordine (calcolo dei predicati).
Si consideri la struttura che ha come supporto l'insieme di tutte le persone e di tutti gli stati ed in cui
si interpreta
- M come Mario
- A come Antonio
- I come l'Italia
- F come la Francia
- persona(x) come "x e' una persona";
- conoscente(x,y) come "x conosce y";
- cittadino(x,y) come "x e' cittadino di y".
Scrivere la fbf il cui valore di verita'
in tale struttura
coincide con quello della seguente frase in italiano:
Tutti i conoscenti comuni a Mario e ad Antonio sono italiani, ma Mario ha anche conoscenti francesi.
(Si hanno a disposizione entrambi i quantificatori e tutti i connettivi logici)
Fare lo stesso con la frase
Tutti i conoscenti comuni a Mario e ad Antonio sono francesi, ma Mario ha anche conoscenti italiani.
Soluzione.
Esercizio 112
Definire la relazione di conseguenza tautologica nella Logica Proposizionale (Calcolo Proposizionale) e dimostrare che
non e' vero che, prese due fbf A e B,
vale la seguente proprieta':
Se ( ⊨ A implica ⊨ B )
allora
A ⊨ B
Soluzione.
Esercizio 113
Sia
{{M0,A0,I0, F0},
{persona1, conoscente2, cittadino2} }
una segnatura per la logica del primo ordine (calcolo dei predicati).
Si consideri la struttura che ha come supporto l'insieme di tutte le persone e di tutti gli stati ed in cui
si interpreta
- M come Mario
- A come Antonio
- I come l'Italia
- F come la Francia
- persona(x) come "x e' una persona";
- conoscente(x,y) come "x conosce y";
- cittadino(x,y) come "x e' cittadino di y".
Scrivere la fbf il cui valore di verita'
in tale struttura
coincide con quello della seguente frase in italiano:
Mario e ad Antonio hanno alcuni conoscenti italiani in comune, ma entrambi conoscono dei francesi.
(Si hanno a disposizione entrambi i quantificatori e tutti i connettivi logici)
Soluzione.
Esercizio 114
Si consideri la segnatura dell'eseercizio 114.
Fornire delle strutture (non banali) nelle quali le seguenti formule risultino vere e strutture nelle quali risultino false.
∀ x. ∀ y.conoscente(x,y)
∃ z. ∀ x. (persona(x) \/ cittadino(F,z))
Soluzione.
Esercizio 115
Sia Numbers il sistema formale definito come segue:
S={0,s,(,),i,N}
W={xiN | x e' una stringa in S*}
Ax={ s(s(0))iN }
R = {pippo, pluto} dove
xiN
(pippo) ---------- in cui x e' una qualsiasi stringa in S*
s(x)iN
s(0)iN
(pluto) --------------
0iN
Definiamo la semantica di Numbers nel seguente modo:
una fbf xiN e' valida quando, interpretando il simbolo '0' come il numero 0 e
's' come la funzione 'incremento di uno', x rappresenta un numero naturale.
Dimostrare che rispetto a questa semantica Numbers e' un sistema corretto.
Numbers e' anche completo? Giustificare adeguatamente la risposta.
La regola pluto e' derivabile? Perche'?
E' ammissibile? Perche'?
Esercizio 115.2
Dimostrare per induzione completa che la regola pluto dell'esercizio precedente
non e' derivabile.
Soluzione. (by FB e Gabriele Stramandino)
Esercizio 116
La seguente e' una dimostrazione (non completamente specificata) di un teorema
(non completamente specificato),
nel sistema formale CL.
Ricopiarla inserendo le parti mancanti.
1. skkk = kk(kk) (?)
2. ?? (axk)
3. skkk = ? (trans)(?,?)
dove gli assiomi e regole di CL sono:
-------(axk) -------------(axs)
kMN=M sMNR=MR(NR)
R=R' MR=NR R=R' RM=RN
---------------(cong1) ---------------(cong2)
MR=NR' RM=R'N
M=N M=N N=R
-----(symm) ---------(trans) ------(refl)
N=M M=R M=M
Quante dimostrazioni si possono avere di questo stesso teorema in CL? Giustificare la risposta.
Soluzione.
Esercizio 117
Avendo a disposizione i seguenti risultati:
Teorema Sia Γ un insieme consistente di fbf di P0,
e sia α tale che Γ ⊬Po α.
Allora Γ ∪ {¬α} e' consistente.
Proposizione Sia δ una fbf di Po. Allora
δ ⊢Po ¬¬δ
Dimostrare che se Γ∪{α} e' contraddittorio allora Γ ⊢Po ¬α.
Esercizio 118
Sia {{},{scontato1, pv1, alcoolico1, costapiu1}}
una segnatura per la logica del primo ordine (calcolo dei predicati).
Si consideri la struttura che ha come supporto l'insieme di tutti i prodotti ed in cui
si interpreta
- scontato(x) come "x e' scontato";
- pv(x) come "x e' un prodotto in vendita";
- alcoolico(x) come "x e' alcoolico";
- costapiu(x) come "x costa piu' di venti euro".
Scrivere la fbf il cui valore di verita'
in tale struttura
coincide con quello della seguente frase in italiano
Gli alcolici in vendita senza sconto costano tutti piu di venti euro, mentre quelli con lo
sconto costano al piu venti euro.
(a-B)
Gli alcolici in vendita con lo sconto costano tutti al piu' venti euro, mentre quelli senza
sconto costano piu' di venti euro.
(Si hanno a disposizione entrambi i quantificatori e tutti i connettivi logici)
Soluzione.
Esercizio 119
Nella logica del primo ordine (calcolo dei predicati),
sia Σ una segnatura.
Definire cos'e' una struttura
AΣ
per Σ.
Esercizio 120
Dimostrare, in deduzione naturale,
P ⊢ (¬ P) → Q
e
P, Q ⊢ ¬ (P → ¬ Q)
Soluzione.
Esercizio 121
Dimostrare che in un sistema formale corretto rispetto una certa semantica, gli assiomi sono validi e le regole
permettono di affermare conclusioni valide se si suppone che le premesse siano valide.
(Per semplicita', consideriamo corretto un sistema formale quando tutti i teoremi sono validi)
Soluzione.
Esercizio 122 Svolgere l'esercizio 121 utilizzando l'induzione completa.
Esercizio 123
Fare un esempio di sistema formale (con la relativa semantica) che sia completo ma non corretto.
Soluzione. (by G.Stramandino)
Esercizio 124
Si consideri la seguente segnatura per la logica dei predicati con uguaglianza
(e con tutti i quantificatori e connettivi logici):
{{z0, exp2},{Nat1, <2}}.
Si consideri inoltre la struttura che abbia
come supporto i numeri reali ed in cui il simbolo di funzione z venga interpretato con il numero 0,
exp
con la funzione
di elevamento a potenza, il predicato Nat con il predicato
essere un numero naturale e il predicato < con minore stretto.
Si fornisca la formula ben formata la cui
interpretazione in tale struttura corrisponda alla seguente affermazione.
Siano a un numero reale non negativo e n un numero naturale.
Allora esiste uno ed un solo numero reale non negativo b tale che
b alla n e' uguale ad a
Soluzione.
Esercizio 125 (non banale)
Dimostrare per induzione matematica sulla lunghezza della derivazione, il seguente enunciato:
Se Γ⊢Dα allora esiste una deduzione
α1 α2 ... αm≡α
che utilizza ipotesi in Γ e tale che
tale che ∀ 1≤i≤m: se αi e' un'ipotesi allora
∀ 1≤j≤i αj e' un'ipotesi.
Informalmente quindi se esiste una derivazione di α con ipotesi Γ allora ne esiste
anche una in cui le ipotesi utilizzate sono tutte all'inizio. E' un enunciato ovvio, che comunque vogliamo
dimostrare formalmente con precisione.
Esercizio 126
La dimostrazione del Corollario 3.2 del testo del Martini [SM] utilizza un passaggio che, pur essendo
abbastanza chiaro, come esercizio vogliamo rendere ulteriormente piu' chiaro.
Il passaggio in questione afferma che, utilizzando la Proposizione 3.8, si puo' mostrare
che se Γ∪ {α} e' contraddittorio, lo e' anche Γ∪ {¬¬α}.
In particolare si dice che utilizzando la Proposizione 3.8 si puo' mostrare che
se Γ,α, ⊢ δ allora
Γ,¬¬α ⊢ δ. Dimostrare in modo preciso (anche se pedante)
tale affermazione.
Esercizio 127
Nella dimostrazione della Proposizione 3.6 del testo del Martini [SM] e' presente una
deduzione in cui, come giustificazione per l'inserimento al punto 6. della fbf
¬α→¬α, e' indicato "proposizione 3.1" (che formalmente non e' una possibile
giustificazione per affermare una fbf in una deduzione). Questo significa che,
per avere una vera deduzione, basta inserire al posto della fbf ¬α→¬α
l'intera deduzione presente nella Proposizione 3.1.
Come alternativa per dimostrare la Proposizione 3.6, basterebbe giustificare
¬α→¬α con "ipotesi", In questo modo avremmo
¬α→¬α, ¬¬α, ⊢ α.
Poiche' dalla proposizione 3.1 sappiamo che ⊢ α→¬α,
possiamo far vedere che ¬¬α, ⊢ α conoscendo che
¬α→¬α, ¬¬α ⊢ α e ⊢ α→¬α.
(Hint: fornire una versione piu' generale della Proposizione 2.3 (dimostrandola) ed utilizzarla
per dimostrare cio' che ci serve).
Esercizio 128
Dimostrare per induzione che, presa una formula α, sostituendo ogni sua sottoformula della forma
¬¬δ con δ, si ottiene una formula che ha lo stesso valore di verita' di α
qualsiasi sia l'assegnamento proposizionale considerato.
Esercizio 129
Ci sono tre sorelle: Agata, Barbara e Concetta. Almeno una di loro e' bionda.
Sappiamo che se Agata e' bionda, lo e' anche Barbara, ed inoltre se Concetta e'
bionda lo e' anche Barbara. Una sola tra Barbara e Concetta e' bionda.
Formalizzare cio' che sappiamo come insieme di ipotesi in Logica Proposizionale,
e dimostrare in Deduzione Naturale, utilizzando tali ipotesi,
che Barbara e' bionda.
Possibile soluzione.
Esercizio 130
Sia {{a0,b0},{c2,p2}} una segnatura dove a e b sono simboli di costante, mentre c e p
sono simboli predicativi binari.
Interpretando a come "Antonella", b come
"Bruno", c(x, y) come "x conosce y", p(x, y) come "x e' parente di y",
traducete la seguente frase (scrivete cioe' la formule ben formata corrispondente):
Un parente di Bruno conosce una persona che conosce qualche parente di Antonella;
Possibile soluzione.
Esercizio 131
Dimostrare, in Deduzione Naturale, che
Soluzione.
Esercizio 132
Sia {{},{c1, g1, p2, a2, =2}} una segnatura dove 'c' e 'g' sono simboli
predicativi unari, mentre 'p', 'a' e '='
sono simboli predicativi binari.
Si consideri una struttura che abbia come supporto l'insieme degli uomini, dei cani e dei gatti ed in cui si interpreti
c(x) come "x e' un cane", g(x) come "x e' un gatto",
p(x,y) come "x e' il padrone di y" e
a(x,y) come "x ama y". Inoltre "=" corrisponde al predicato di identita'.
Tradurre le seguenti frasi (scrivete cioe' le formule ben formate che hanno lo stesso valore di verita' rispetto alla struttura fornita),
avendo a disposizione entrambi i quantificatori e tutti i connettivi logici:
(i) cani e gatti non si amano;
(ii) tutti i cani e i gatti, se lo hanno, hanno un solo padrone;
Scrivere inoltre la frase in italiano corrispondente alla seguente formula ben formata:
∀x.((c(x) ∧ ∃y.p(y,x)) → ∃z. a(z,x))
Soluzione.
Esercizio 133
Dimostrare in deduzione naturale per la logica proposizionale la proposizione 3.10 del testo di Martini,
cioe' che α → β ⊢ β → α
Soluzione.
Esercizio 134
Dimostrare, in Deduzione Naturale, che
Soluzione.
Esercizio 135
Sia {{a0,b0},{c2,p2}} una segnatura dove a e b sono simboli di costante, mentre c e p
sono simboli predicativi binari.
Interpretando a come "Antonella", b come
"Bruno", c(x, y) come "x conosce y", p(x, y) come "x e' parente di y",
traducete la seguente frase (scrivete cioe' la formule ben formata corrispondente):
Ogni parente di Bruno conosce una persona che conosce qualche parente di Antonella.
Soluzione.
Esercizio XX
Soluzione.
Esercizio XX
Soluzione.
Esercizio XX
Soluzione.