ESERCIZIO 4.1. Si consideri la seguente definizione di
funzione
f 100 = 0
f n = if n > 100 then n + f 0 else f (n+1) – 1
Dimostrare che f è totale e che coincide con la
funzione intera g(x) = x –100.
Per la risoluzione procediamo per induzione sulla precedenza
indotta dalla definizione, stabilendo come minimale n = 100.
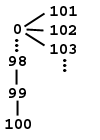
Il diagramma di precedenza della relazione [ è:

CASO BASE: f 100 = 0 = g 100
CASO INDUTTIVO:
1° CASO: n > 100
f n = n + f 0 {dato che 0 [ n} => f n = n + g 0 = n + 0 - 100
= n - 100
2° CASO: n < 100
f n = f (n+1) -1 {dato che n +1 [ n } => f n = n +1 - 100 -1 =
n - 100
La funzione f(x) coincide con la funzione g(x), così come dimostrato e inoltre, secondo il Teorema di Terminazione (4.2) essa è totale, poichè è ben fondata e definita su tutti i minimali.