\n
p, ul, ol, li {font-family:Arial; font-size:8pt; font-weight:normal;)\n
h1 {font-family:Arial; font-size:14pt; font-weight:bold;) \n
h2 {font-family:Arial; font-size:12pt; font-weight:bold;) \n
h3 {font-family:Arial; font-size:10pt; font-weight:bold;) \n
strong {font-family:Arial; font-size:8pt; font-weight:bold;) \n
em {font-family:Arial; font-size:8pt; font-weight:italic;) \n
";
$linux_stile="
";
?>
poincarè
Modelli di Poincaré e Minkowski della geometria iperbolica
La presente esposizione non é una introduzione alla geometria iperbolica,
ma si propone i seguenti obiettivi
- fornire esempi non banali riguardanti la geometria riemanniana, introdotta
nella prima parte del corso di Fisica Matematica II;
- descrivere in maniera piú precisa le superfici tridimensionali
di curvatura
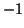 che si incontrano nel modello cosmologico aperto di Friedmann-Robertson-Walker,
nella seconda parte del corso di Fisica Matematica II;
che si incontrano nel modello cosmologico aperto di Friedmann-Robertson-Walker,
nella seconda parte del corso di Fisica Matematica II;
- mostrare un collegamento tra la geometria riemanniana (pseudo-riemanniana)
e le geometrie non euclidee, anche come stimolo per approfondire quest'ultimo
argomento;
- mostrare che il gruppo di simmetria piú naturale per le superfici
a curvatura costante negativa, non é quello delle rotazioni, ma quello
di Lorentz.
Gaetano Moschetti
2002-01-06
