Nello spazio-tempo di Minkowski tridimensionale, le isometrie che che lasciano fissa l'origine (le analoghe delle
rotazioni in una metrica euclidea) sono le trasformazioni di Lorentz, cioé quelle trasformazioni determinate dalle
matrici
![]() tali che
tali che
![]() , dove
, dove ![]() é la matrice associata
alla metrica (13) nelle coordinate
é la matrice associata
alla metrica (13) nelle coordinate ![]() . Le superfici invarianti per trasformazioni di Lorentz sono le
superfici di equazione
. Le superfici invarianti per trasformazioni di Lorentz sono le
superfici di equazione
![]() . In particolare per
. In particolare per ![]() , si ottiene l'iperboloide
, si ottiene l'iperboloide
![]() , la cui
falda superiore (
, la cui
falda superiore (![]() ) é il modello di Minkowski visto precedentemente. Escludendo le trasformazioni non-ortocrone
(
) é il modello di Minkowski visto precedentemente. Escludendo le trasformazioni non-ortocrone
(
![]() ) che mandano la falda superiore dell'iperboloide nella falda inferiore e viceversa, il sottogruppo
delle trasformazioni ortocrone (
) che mandano la falda superiore dell'iperboloide nella falda inferiore e viceversa, il sottogruppo
delle trasformazioni ortocrone (
![]() ) é un gruppo di isometrie per la metrica (15) del modello
di Minkowski. Si puó dimostrare che, viceversa ogni trasformazione che lascia invariata la falda
) é un gruppo di isometrie per la metrica (15) del modello
di Minkowski. Si puó dimostrare che, viceversa ogni trasformazione che lascia invariata la falda ![]() dell'iperboloide
dell'iperboloide
![]() deve essere una trasformazione di Lorentz ortocrona.2
deve essere una trasformazione di Lorentz ortocrona.2
Poiché le trasformazioni di Lorentz ortocrone agiscono transitivamente sul modello di Minkowski, esse sono isometrie su quest'ultimo e vengono proiettate tramite le isometrie (16) o (17) in isometrie sul disco di Poincaré.
Utilizzando le conclusioni precedenti, determiniamo l'espressione analitica di tali isometrie sul disco di Poincaré.
A tal fine, consideriamo, il sottogruppo ![]() delle trasformazioni di Lorentz ortocrone e pari:
delle trasformazioni di Lorentz ortocrone e pari:
![]() . Tali trasformazioni verranno chiamate proprie e resta inteso che, nel seguito, anche se
non espressamente specificato, verranno considerate solo trasformazioni proprie. Le trasformazioni dispari sono ottenute
componendo quelle pari con un'inversione di uno degli assi spaziali, ció dá luogo a delle riflessioni.
. Tali trasformazioni verranno chiamate proprie e resta inteso che, nel seguito, anche se
non espressamente specificato, verranno considerate solo trasformazioni proprie. Le trasformazioni dispari sono ottenute
componendo quelle pari con un'inversione di uno degli assi spaziali, ció dá luogo a delle riflessioni.
Denotiamo con ![]() le coordinate euclidee (
le coordinate euclidee (![]() ) dei punti di
) dei punti di ![]() e con
e con
![]() , le
coordinate minkowskiane (
, le
coordinate minkowskiane (
![]() ) dei punti di
) dei punti di ![]() . La trasformazione (16) in tali
coordinate si scrive
. La trasformazione (16) in tali
coordinate si scrive
la quale a sua volta si inverte facilmente:
La piú generale trasformazione di Lorentz propria in ![]() dimensioni é data dalla composizione tra rotazioni di asse
dimensioni é data dalla composizione tra rotazioni di asse
![]() e trasformazioni speciali di Lorentz, cioé trasformazioni spazio-temporali che lasciano fisso un asse
spaziale passante per l'origine. Denotiamo con
e trasformazioni speciali di Lorentz, cioé trasformazioni spazio-temporali che lasciano fisso un asse
spaziale passante per l'origine. Denotiamo con
![]() con
con
![]() , la trasformazione speciale
, la trasformazione speciale
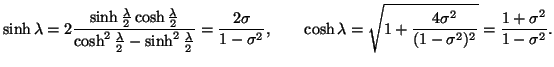
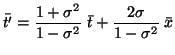
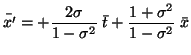
La piú generale trasformazione speciale attorno alla retta ![]() appartenente al piano
appartenente al piano ![]() , passante per
l'origine e formante l'angolo
, passante per
l'origine e formante l'angolo ![]() con l'asse
con l'asse ![]() é data dal prodotto
é data dal prodotto
![]() , dove
, dove
![]() é la rotazione di asse
é la rotazione di asse ![]() e angolo
e angolo ![]() , quindi é determinata dalla matrice
, quindi é determinata dalla matrice
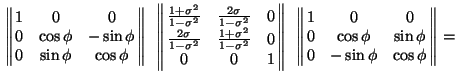
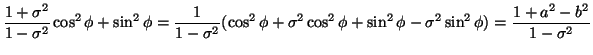
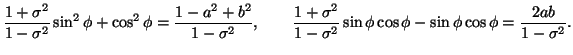
Cosí la matrice (21) si puó anche scrivere
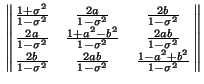 |
(22) |
Proiettando, mediante le (19) (20), la trasformazione (23) sul disco di Poincaré, si ottengono le seguenti trasformazioni:
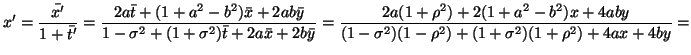

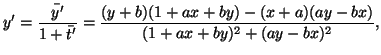
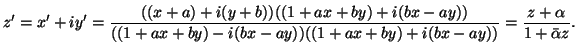
Si puó perció concludere che le isometrie del disco di Poincaré corrispondenti alle trasformazioni speciali di Lorentz sono rappresentate dalla trasformazione
La trasformazione (24), che é una particolare trasformazione di Moebius, gode delle seguenti proprietá:
Nel caso euclideo, le isometrie proprie sono le traslazioni e le rotazioni. Le prime hanno un punto fisso improprio,
mentre le altre hanno un punto fisso proprio. Cosí la trasformazione (24), i cui punti fissi sono impropri
é equiparabile alle traslazioni euclidee, ed é chiamata iperbolica. La differenza tra le traslazioni euclidee
e le trasformazioni iperboliche sta nel numero dei punti fissi, ma ció é scontato, perché nel piano euclideo ogni
retta ha un solo punto improprio, mentre nel disco di Poincaré ogni geodetica incontra la
![]() in due punti
distinti, quindi, fissata una traslazione, essa lascia una direzione invariante e quindi, nel caso euclideo, lascia
fisso un punto improprio, mentre nel caso iperbolico lascia fissi i due punti impropri della retta che individua tale
direzione.
in due punti
distinti, quindi, fissata una traslazione, essa lascia una direzione invariante e quindi, nel caso euclideo, lascia
fisso un punto improprio, mentre nel caso iperbolico lascia fissi i due punti impropri della retta che individua tale
direzione.
Fino ad ora sono state considerate le trasformazioni speciali di Lorentz nello spazio-tempo di Minkowski tridimensinale,
ma si é detto prima che la piú generale trasformazione di Lorentz é generata, oltre che da quest'ultime, anche
dalle rotazioni spaziali di asse ![]() . É immediato verificare che la composizione di una rotazione di angolo
. É immediato verificare che la composizione di una rotazione di angolo
![]() ed asse
ed asse ![]() , con le proiezioni (19) (20), dá come risultato la trasformazione su
, con le proiezioni (19) (20), dá come risultato la trasformazione su ![]() :
:
![]() , che é l'analoga della rotazione euclidea perché ha come punto fisso l'origine. Una
trasformazione con un solo punto fisso proprio si chiama ellittica.
, che é l'analoga della rotazione euclidea perché ha come punto fisso l'origine. Una
trasformazione con un solo punto fisso proprio si chiama ellittica.
Si puó cosí concludere che le isometrie elementari sul disco di Poincaré, ottenute, con il precedente meccanismo, dalle trasformazioni di Lorentz tridimensionali, sono date dalla funzione
La (25), che ha il vantaggio di evidenziare il modo in cui si compongono le rotazioni é le traslazioni, si puó anche scrivere sotto forma di una trasformazione di Moebius che semplifica la classificazione delle isometrie descritte dalla (25):
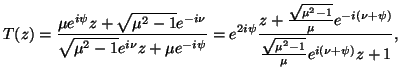
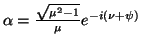 , si ottiene la (25).
Viceversa dalla (25) con
, si ottiene la (25).
Viceversa dalla (25) con
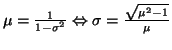 ,
,
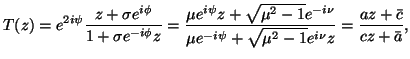
Per classificare le possibili isometrie descritte dalle (25) (26), determiniamo i punti fissi di quest'ultima, cioé le soluzioni dell'equazione
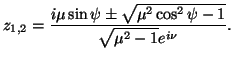 |
(27) |
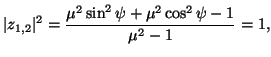
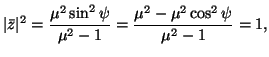
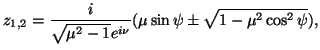
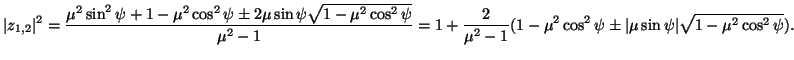
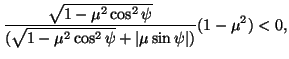
Mentre le trasformazioni iperboliche ed ellittiche, sono analoghe alle traslazioni e rotazioni euclidee, la
trasformazione parabolica non ha nessuna controparte euclidea. Per determinare un esempio di tale trasformazione,
consideriamo il caso in cui il punto fisso sia ![]() . In questo caso i numeri complessi che determinano la trasformazione
. In questo caso i numeri complessi che determinano la trasformazione
![]() e
e
![]() , sono soggetti ai seguenti due vincoli:
, sono soggetti ai seguenti due vincoli:
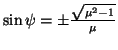 , da cui si ricava
, da cui si ricava
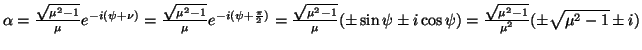 .
.