

Next: Geodetiche per due punti
Up: Modello di Poincaré
Previous: Modello di Poincaré
Il modello di Poincaré del piano iperbolico é costituito dal disco unitario 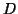 del piano euclideo con
metrica
del piano euclideo con
metrica
 |
(1) |
rispetto ad un sistema di coordinate cartesiane ortogonali con origine nel centro 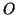 di
di 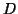 . La metrica
(1), in coordinate polari
. La metrica
(1), in coordinate polari
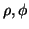 centrate in
centrate in 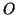 , assume la forma
, assume la forma
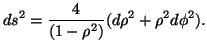 |
(2) |
La metrica (2) ammette equazioni delle geodetiche facilmente integrabili. Infatti, rispetto ad un parametro
affine, la seconda equazione é
la quale é immediatamente integrabile:
essendo  una costante arbitraria.
Se
una costante arbitraria.
Se 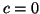 , allora
, allora  , quindi
, quindi
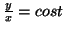 , cioé si ottiene come soluzione un diametro di D.
Quindi nel seguito si puó supporre
, cioé si ottiene come soluzione un diametro di D.
Quindi nel seguito si puó supporre  . Dall'equazione precedente si ricava
. Dall'equazione precedente si ricava
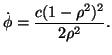 |
(3) |
D'altra parte la prima equazione puó essere rimpiazzata dall'integrale primo (dell'energia)1
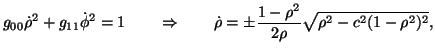 |
(4) |
che assieme alla (3) dá
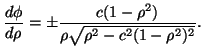 |
(5) |
Posto
la (5) diventa
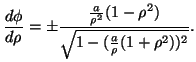 |
(6) |
Con la sostituzione
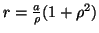 , essendo
, essendo
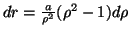 , si ha
, si ha
da cui, posto
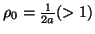 , si ricava
, si ricava
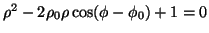 e quindi,
tenendo conto che le soluzioni col segno
e quindi,
tenendo conto che le soluzioni col segno 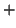 danno
danno 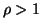 , cioé traiettorie esterne a
, cioé traiettorie esterne a 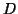 , si ottiene
, si ottiene
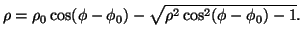 |
(7) |
La generica circonferenza di centro 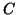 di coordinate polari
di coordinate polari
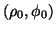 e raggio
e raggio 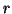 , che interseca
ortogonalmente il bordo
, che interseca
ortogonalmente il bordo  di
di 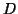 , deve verificare l'equazione della fig.1.
, deve verificare l'equazione della fig.1.
Figure 1:
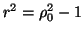
|
|
In base alla fig.2 si trova l'equazione di tale circonferenza in coordinate polari, che considerata
insieme all'equazione della fig.1, dá:
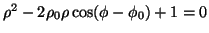 , cioé l'equazione delle
geodetiche, di cui la parte che interseca
, cioé l'equazione delle
geodetiche, di cui la parte che interseca 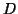 (
(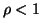 ) é quella con il segno meno, cioé la (7).
Nella (7) imponendo
) é quella con il segno meno, cioé la (7).
Nella (7) imponendo 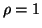 si ottiene,
si ottiene,
 da cui si riconosce che gli
estremi di tale geodetica si ottengono per
da cui si riconosce che gli
estremi di tale geodetica si ottengono per
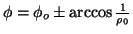 .
.
Figure:
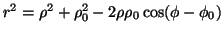
|
|
Si puó quindi concludere che:
Le geodetiche della metrica (2) sono:
- i diametri di
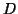 ,
,
- gli archi di circonferenza che intersecano ortogonalmente il bordo di
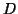 e precisamente tutte e sole le
curve che verificano l'equazione (7) con
e precisamente tutte e sole le
curve che verificano l'equazione (7) con
![$ \phi\in[\phi_0-\arccos\frac{1}{\rho_0},
\phi_0+\arccos\frac{1}{\rho_0}]$](img47.gif)
D'altra parte, tenendo conto che la metrica (1) é conforme a quella del piano euclideo, si puó concludere
che:
Gli angoli formati tra due geodetiche incidenti in un punto  , sono uguali a quelli euclidei formati dalle
tangenti in
, sono uguali a quelli euclidei formati dalle
tangenti in  .
.
Footnotes
- ... (dell'energia)1
- supporre uguale
ad 1 la costante arbitraria al secondo membro, equivale a scegliere, come parametro affine sulla geodetica, l'ascissa
curvilinea.


Next: Geodetiche per due punti
Up: Modello di Poincaré
Previous: Modello di Poincaré
2002-02-25
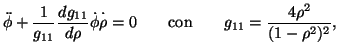
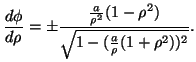
![]() , essendo
, essendo
![]() , si ha
, si ha
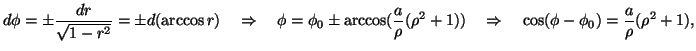
![]() di coordinate polari
di coordinate polari
![]() e raggio
e raggio ![]() , che interseca
ortogonalmente il bordo
, che interseca
ortogonalmente il bordo ![]() di
di ![]() , deve verificare l'equazione della fig.1.
, deve verificare l'equazione della fig.1.
![]() , cioé l'equazione delle
geodetiche, di cui la parte che interseca
, cioé l'equazione delle
geodetiche, di cui la parte che interseca ![]() (
(![]() ) é quella con il segno meno, cioé la (7).
Nella (7) imponendo
) é quella con il segno meno, cioé la (7).
Nella (7) imponendo ![]() si ottiene,
si ottiene,
![]() da cui si riconosce che gli
estremi di tale geodetica si ottengono per
da cui si riconosce che gli
estremi di tale geodetica si ottengono per
![]() .
.
![]() , sono uguali a quelli euclidei formati dalle
tangenti in
, sono uguali a quelli euclidei formati dalle
tangenti in ![]() .
.