

Next: Distanza tra due punti
Up: Modello di Poincaré
Previous: Metrica e geodetiche
In coordinate cartesiane l'equazione della circonferenza di centro
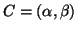 e raggio
e raggio 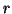 é
é
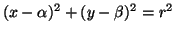 cioé
cioé
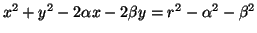 . Quindi, denotate con
. Quindi, denotate con
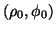 le coordinate polari di
le coordinate polari di  , l'equazione diventa
, l'equazione diventa
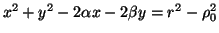 , ed
imponendo la condizione di ortogonalitá
, ed
imponendo la condizione di ortogonalitá
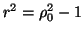 a
a
 , vista nella sezione precedente, si puó
concludere che
, vista nella sezione precedente, si puó
concludere che
esiste solo una sola circoferenza di centro
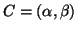 ortogonale a
ortogonale a
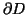 ed ha equazione
ed ha equazione
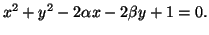 |
(8) |
Dati due punti distinti
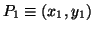 e
e
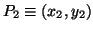 , si possono presentare le seguenti eventualitá:
, si possono presentare le seguenti eventualitá:
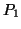 e
e 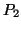 sono allineati con l'origine (
sono allineati con l'origine (
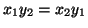 ), questo significa che per essi passa
uno ed un sol diametro di
), questo significa che per essi passa
uno ed un sol diametro di 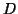 , cioé, in accordo con la sezione precedente, una ed una sola geodetica;
, cioé, in accordo con la sezione precedente, una ed una sola geodetica;
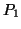 e
e 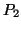 non sono allineati con l'origine (
non sono allineati con l'origine (
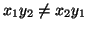 ), allora, imponendo che essi siano soluzioni
dell'equazione (8), per il teorema di Kramer, si trova che determinano univocamente la coppia
), allora, imponendo che essi siano soluzioni
dell'equazione (8), per il teorema di Kramer, si trova che determinano univocamente la coppia
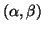 :
:
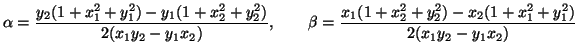 |
(9) |
e quindi ll'unica geodetica passante per essi.
In particolare, se i punti vengono assegnati in coordinate polari:
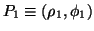 e
e
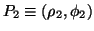 ,
allora, con facili calcoli, si vede che le equazioni (9) si trasformano nelle seguenti:
,
allora, con facili calcoli, si vede che le equazioni (9) si trasformano nelle seguenti:
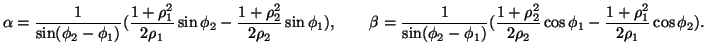 |
(10) |
Infine se si vuol determinare l'equazione della geodetica passante per 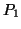 e
e 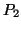 nella forma (7), basta ricavare
le coordinate polari
nella forma (7), basta ricavare
le coordinate polari
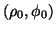 di C dalle coordinate cartesiane
di C dalle coordinate cartesiane
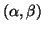 .
.


Next: Distanza tra due punti
Up: Modello di Poincaré
Previous: Metrica e geodetiche
2002-02-25
![]() ortogonale a
ortogonale a
![]() ed ha equazione
ed ha equazione
![]() e
e
![]() ,
allora, con facili calcoli, si vede che le equazioni (9) si trasformano nelle seguenti:
,
allora, con facili calcoli, si vede che le equazioni (9) si trasformano nelle seguenti:
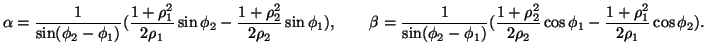
![]() e
e ![]() nella forma (7), basta ricavare
le coordinate polari
nella forma (7), basta ricavare
le coordinate polari
![]() di C dalle coordinate cartesiane
di C dalle coordinate cartesiane
![]() .
.