Poiché il disco ![]() con la metrica (1) é una varietá riemanniana, esso é, come é noto, metrizzabile,
definedo la distanza
con la metrica (1) é una varietá riemanniana, esso é, come é noto, metrizzabile,
definedo la distanza ![]() tra due punti
tra due punti ![]() e
e ![]() , come la lunghezza del segmento geodetico che li congiunge, per
misurare la quale basta utilizzare come parametro sulla geodetica l'ascissa curvilinea.
, come la lunghezza del segmento geodetico che li congiunge, per
misurare la quale basta utilizzare come parametro sulla geodetica l'ascissa curvilinea.
Come prima cosa supponiamo che ![]() e
e ![]() siano allineati con il centro di
siano allineati con il centro di ![]() e, tanto per fissare le idee, supponiamo
che stiano sullo stesso raggio (
e, tanto per fissare le idee, supponiamo
che stiano sullo stesso raggio (
![]() ), allora l'equazione (4), per
), allora l'equazione (4), per
![]() , si scrive
, si scrive

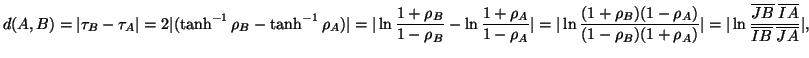
Se invece i punti ![]() e
e ![]() , pur appartenendo allo stesso diametro, si trovano disposti come nalla seconda delle
fig.3 (
, pur appartenendo allo stesso diametro, si trovano disposti come nalla seconda delle
fig.3 (
![]() ), essendo
), essendo ![]() la distanza da
la distanza da ![]() , ed avendo fissato come origine dell'ascissa
curvilinea
, ed avendo fissato come origine dell'ascissa
curvilinea ![]() , si ha:
, si ha:
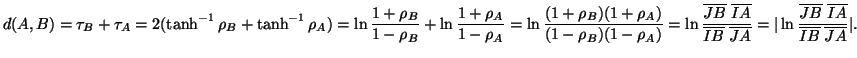
Consideriamo ora il caso in cui i due punti ![]() e
e ![]() non siano allineati con il centro, come in fig. 4, denotiamo
con
non siano allineati con il centro, come in fig. 4, denotiamo
con ![]() l'unica geodetica che li congiunge e sia
l'unica geodetica che li congiunge e sia
![]() il centro della circonferenza del piano
euclideo di cui essa é un arco. Denotiamo come in fig:4 con
il centro della circonferenza del piano
euclideo di cui essa é un arco. Denotiamo come in fig:4 con ![]() e
e ![]() gli estremi di
gli estremi di ![]() e con
e con ![]() il
punto in cui il segmento
il
punto in cui il segmento
![]() interseca
interseca ![]() . Sia
. Sia ![]() l'ascissa curvilinea su
l'ascissa curvilinea su ![]() con origine in
con origine in
![]() ed avente come verso crescente quello che va da
ed avente come verso crescente quello che va da ![]() verso
verso ![]() .
.
Allora, se ![]() é un qualunque punto di
é un qualunque punto di ![]() , denotate con
, denotate con
![]() la sua ascissa
curvilinea e con
la sua ascissa
curvilinea e con
![]() la sua distanza da
la sua distanza da ![]() , per la (5), si trova
, per la (5), si trova

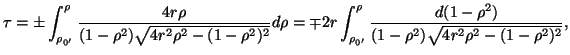
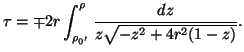
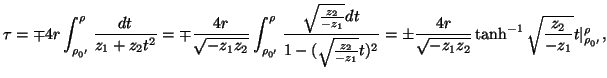
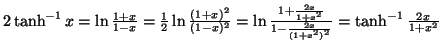 , si ricava che
, si ricava che
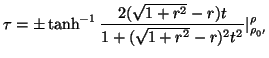
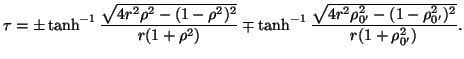
D'altra parte, se come prima si denota con
![]() la lunghezza euclidea del segmento(rettilineo) di estremi
la lunghezza euclidea del segmento(rettilineo) di estremi
![]() e
e ![]() , allora facendo riferimento alla fig. 5, indicando con
, allora facendo riferimento alla fig. 5, indicando con ![]() ,
, ![]() e
e ![]() le anomalie,
rispettivamente dei punti
le anomalie,
rispettivamente dei punti ![]() ,
, ![]() e
e ![]() , si ha:
, si ha:
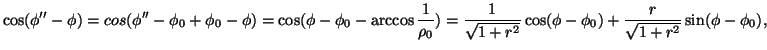
Analogamente
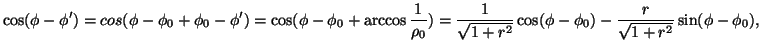
Quindi
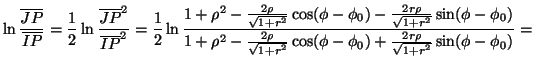
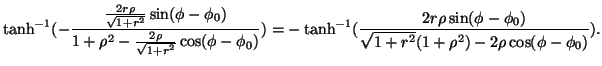
Poiché l'equazione (7) implica
![]() , allora
, allora
![]() e
e
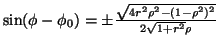 , dove
va preso il segno
, dove
va preso il segno ![]() se
se
![]() cioé, in base alla fig.5, se
cioé, in base alla fig.5, se ![]() appartiene all'arco
appartiene all'arco ![]() .
Quindi
.
Quindi
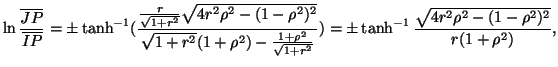
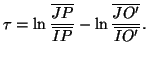 |
(11) |
Si puó cosí concludere che
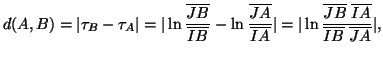 |
(12) |
la distanza di due punti ![]() e
e ![]() é data dal valore assoluto del logaritmo della distanza incrociata dagli
estremi della geodetica a cui appartengono.
é data dal valore assoluto del logaritmo della distanza incrociata dagli
estremi della geodetica a cui appartengono.