the 3x+1 Problem

misty origins:

• Collatz (1932) proposed another problem (of similar nature, still open), yet ...
• proposed by Thwaites (1952), with a 1000-pound prize
• rediscovered several times, whereby it is known under several names: Collatz, Syracuse, Kakutani, Hasse, Ulam, 3x+1, ...

official statement of the Problem: let f : N₊ → N₊ be defined by the following rules:

• fx = 3x + 1   if x is odd
• fx = x/2      if x is even

is it true that repeated iteration of f always converges to 1 ?

or, in other words, that f^* has the 1 → 4 → 2 → 1 cycle as (unique) attractor?

Mathematics is not yet ready for such problems (Erdös)

3x+1 trajectories and records

this work does not aim at solving the 3x+1 Problem

• a positive answer is conjectured

subject of interest here is the dynamical behaviour of f^*

basic concepts relating to the f^* dynamics:

• trajectory at (origin) x : the infinite sequence x, fx, f²x, ...
• delay of (trajectory at) x : the smallest n such that fⁿx = 1
• delay class d : the set of those x which have delay d
  • remark : every delay class is populated (2^d has delay d )
• class record (CR): the smallest member of a delay class
• delay record (DR): an x such that every y < x has a lower delay
  • fact : every DR is a CR (but the converse does not hold)

distributed search of class records

the assessment that an x is a CR requires certainty that no lower y has the same delay

• → computation of delay(y) for all y < x ?

not really, since several laws relate delays of joining trajectories

• e.g. for all x : delay(2x) = delay(x) + 1,
• and: delay(2x + 1) = delay(6x + 4) + 1 = delay(3x + 2) + 2

such laws may speed-up delay computation, yet CR finding does need exhaustive search

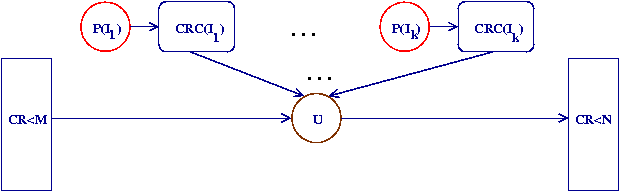
this is easily parallelized by partitioning the search space into disjoint intervals, explored by independent jobs, each producing its own set of CR candidates

• smallests members, in the given interval, of each delay class

the final merge of distributed search results thus amounts to select the best, i.e. smallest, candidate for each delay class

motivation for the search on the Cometa grid

a distributed search effort, to find 3x+1 class records, is active since quite a few years

it has found 2014 CRs so far, exploring the search space up to 57780^.10¹²

• so, why taking the search to the COMETA grid?

4 good reasons:

• (proprietary) OS dependence
• machine architecture dependence (32-bit, vendor-specific)
• design of novel optimization mechanisms, afforded by 64-bit architecture
• simple parallelization structure (DAG partitioning), easy space-time tradeoff

and, last but not least:

• educational use: parallel programming methodology, grid job control & monitoring

a basic parallel algorithm

assume all CRs below M are known

goal: find all new CRs below N > M

• partition the search space [M, N [ into k pairwise disjoint intervals
• for each interval, find the best CR candidates, relatively to that interval
  • that is, regardless of known CRs and of candidates from other intervals
• after all intervals are searched out, merge the parallel search outcomes
  • also taking known CRs into account

optimization (1): Sieving

the heart of CR finding is the delay computation function

• its execution speed is performance critical

the fastest execution is that which... need not start :)

coalescence of trajectories entails that
CRs fall outside certain congruence classes

• for example, 5 is the only CR in the congruence class 5 (mod 8)... why?

for n>0, the trajectories of 8n+5 and 8n+4 coalesce at 6n+4 after the same number of steps (3), so delay(8n+5) = delay(8n+4) → 8n+5 cannot be a CR

this generalizes to congruence classes (2^k-2 + (k mod 2)2^k-1 - 1) (mod 2^k), for k > 2

• checking the general case? hardly efficient...

better off with a finite approximation (e.g. k=18), efficiently implemented by a sieve

optimization (2): Tail cut-off

all trajectories leading to 1 (veritably all, thus) sooner or later fall below 2^t, for any given, fixed t

delay computation may thus get quicker by storing all delay(n) for n < 2^t, and then adding delay(n) to the partially computed delay of x as soon as the trajectory starting at x reaches such an n

• how to choose the tail cut-off threshold parameter t ?

by similar, architecture-dependent data as for the sieve size:

• available RAM size ?

a surely lower threshold proves optimal (t between 12 and 16, usually), that depends on

• cache size !

optimization (3): Head cut-off

two DRs are consecutive if there is no DR in between them

• if x₁ < x₂ is a pair of consecutive DRs, then x < x₂ → delay(x) ≤ delay(x₁)

one can use this to stop the delay computation of hopeless trajectories ahead of time:

• assume all CRs below M are known
• let u be the smallest delay class whose CR is not below M
• x ≥ M may only be a CR if its delay is at least u
• if the trajectory of x falls below x₂ after d steps, then delay(x) ≤ d + delay(x₁)
• hence, if d + delay(x₁) < u, then x cannot be a CR

virtue of this technique: self-optimizing! CR search progress eventually leads to

• raise u → higher cut-off rate
• get higher pairs of consecutive DRs → earlier head cut-off

Head and Tail cut-off in a picture

optimization (4): Acceleration

a small acceleration of delay computation comes from replacing the function f with T, defined as f on the even numbers, whereas for odd x one has

• Tx = (3x + 1)/2 = x + ⌈x/2⌉

clearly, if the T-trajectory from x to 1 has D applications of this rule and E applications of the halving rule, then delay(x) = 2D + E

the interest in T comes from the existence of a permutation of the residues (mod 2^k), defined by the k-prefix of the so-called parity vector of T-trajectories, viz. the binary sequence, dependent on x, defined by v_i(x) = (T ⁱx) mod 2

• the k-prefix of v_i(x) only depends on x (mod 2^k)

thus one may define 2^k distinct k-step composites of T, and decide which applies to x by only looking at x (mod 2^k) : not so small acceleration, by clever programming techniques

interference and smoothening of Acceleration

optimal k for Acceleration depends on cache size, but:

• unconstrained Acceleration reduces the effectiveness of Head cut-off!

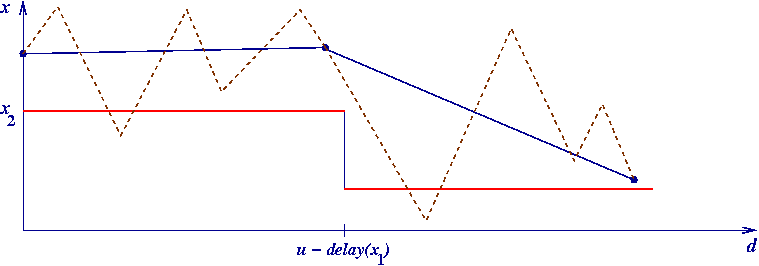
solution: smoothening of Acceleration, that is, shorten Acceleration extent

• for those composites which may cause interference
• below appropriate, Head cut-off dependent thresholds

performance figures

approximate average CPU time h (in hours) to search an interval of size 2⁴⁴, in the neighbourhood of 2⁵⁶:

•     u               h
• 1925         160
• 1951         150
• 1964         148
• 1985         124

remark: the latest performance gain is also due to the introduction of a new pair of consecutive DRs, which has nearly doubled the highest Head cut-off threshold

state of the search and results

search started on 25/09/2007, from 2⁵⁵ + 72 * 2⁴⁸

• as of today, all CRs below 2⁵⁶ + 14 * 2⁴⁸ have been found, which means:
• 18 new CRs, including R₂₀₀₀: challenge candidate confirmed
• one of them truly new, that is, lower than the best known candidate until its discovery:

questions?