General-purpose programming on GPU

Benchmarking, profiling and optimization

Giuseppe Bilotta, Eugenio Rustico, Alexis Hérault

DMI — Università di Catania
Sezione di Catania — INGV

Benchmarking

To benchmark a kernel execution, we use events. Events are like checkpointing stopwatches in GPU streams.

Defining events:

float runtime;
cudaEvent_t start, stop;
cudaEventCreate(&start);
cudaEventCreate(&stop);

Using events:

cudaEventRecord(start, 0);
/* launch kernel */
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&runtime, start, stop);

Destroying events:

cudaEventDestroy(stop);
cudaEventDestroy(start);

Optimization tips

The GPU offers the best performance when all cores are computing. Optimization revolves around three main points:

• maximize parallelism
• minimize memory access latency
• maximize instruction throughput

Maximize parallelism

• use all the GPU cores;
• keep serialization local;
• hide bus latency.

Using all the cores requires a large number of blocks (at least as many as there are MP on the GPU). On devices with capability 2.x, you can launch two kernels.

If you need to serialize (threads must depend on what other threads do), try to keep dependent threads on the same block: you can then use __syncthreads() instead of requiring separate kernel launches.

Hiding latency exploit parallelism between GPU components: if there are warps that can be dispatched while other warps wait, the latency is covered.

Latency hiding requires knowledge of how the instructions are dispatched, which depends on the device capability:

• capability 1.x: 1 instruction per warp over 4 cycles, 1 warp at a time => N instructions hide 4N cycles
• capability 2.0: 1 instruction per warp over 2 cycles, 2 warps at a time => N instructions hide N cycles
• capability 2.1: 2 instructions per warp over 2 cycles, 2 warps at a time => N instructions hide N/2 cycles

A typical instruction takes 22 cycles to complete. This means that 6 warps (capability 1.x) or 22 warps (capability 2.x) are the minimum to hide standard sequential execution (an instruction depending on the result of the previous instruction).

Global and local memory access takes 400 to 800 cycles. Warps needed to hide this latency depend on the density between instructions that do not depend on such memory and instructions that do depend on them.

When using synchronization, all warps in a block are stalled and their latency is that of the worst thread. This is covered by having more than one block per MP.

The occupancy (resident warps/maximum resident warps) can be computed using the CUDA Occupancy Calculator. A higher occupancy helps hiding synchronization latencies.

Minimizing memory latency

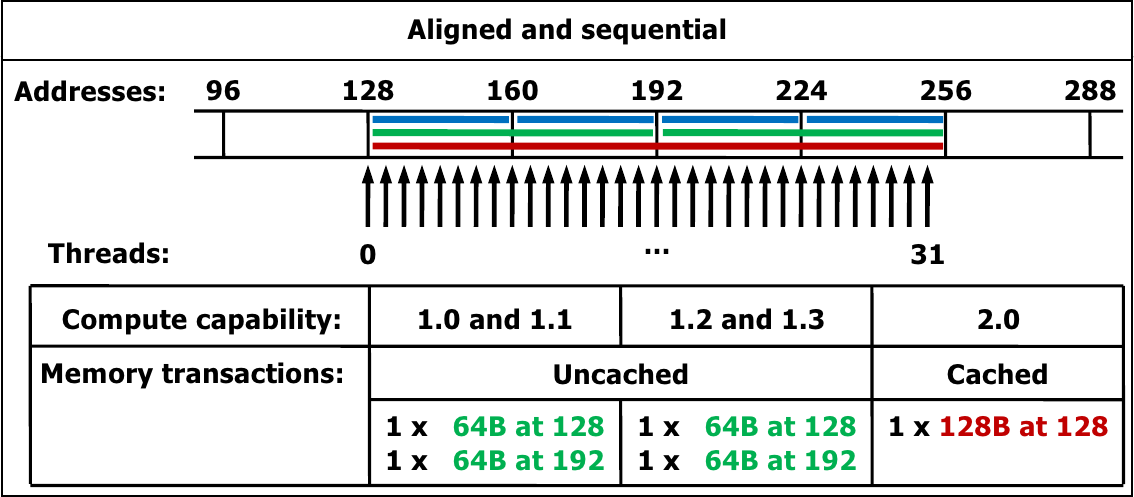
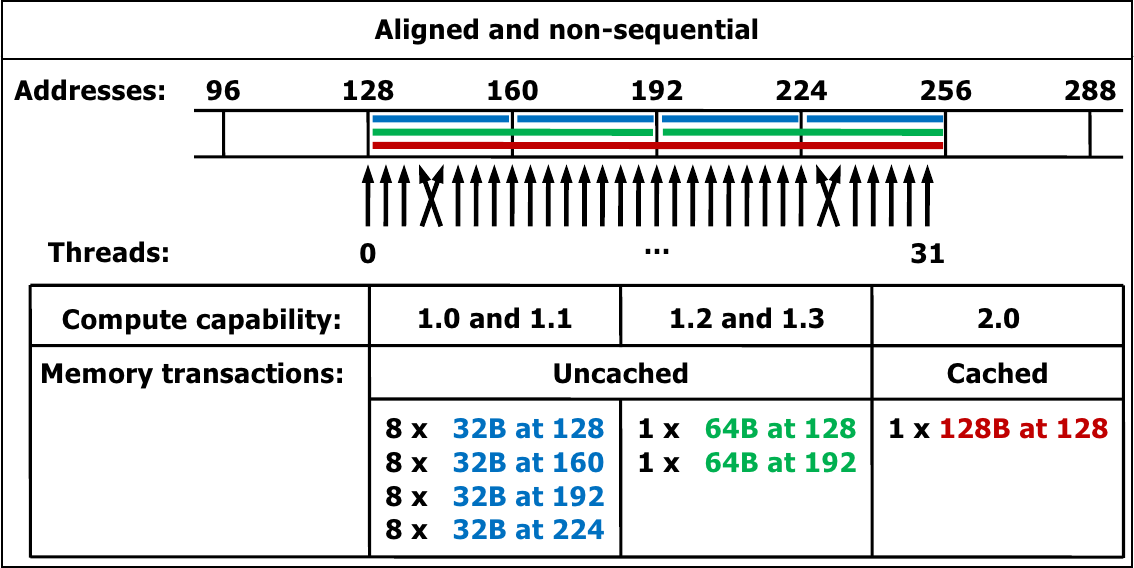
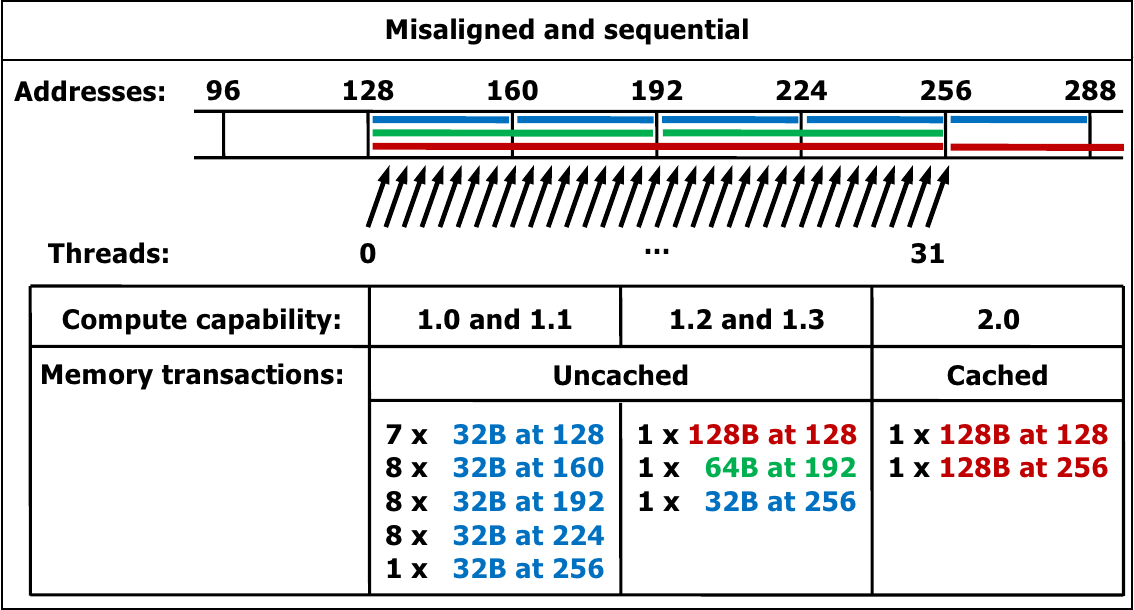
Memory accesses are managed in transactions. A single transaction accesses 32, 64 or 128 bytes, aligned to their size (e.g. 128-byte transactions must be aligned at a 128-byte boundary).

Memory access instructions are automatically managed in transactions. The number of transactions needed for memory accesses depend on:

• data types
• data alignment
• hardware capability

A single memory instruction is issued to access powers-of-two bytes (1 to 16) which are naturally aligned. All other accesses are split in multiple instructions.

cudaMalloc() returns memory which is aligned at 256 bytes.

Row alignment for linearized 2D arrays can be improved using cudaMallocPitch():

data_t *devData; /* e.g. float *devData */
size_t pitch;
cudaMallocPitch(&devData, &pitch, numCols*sizeof(data_t), numRows);

The pitch is in bytes. Element (row, col) is then accessed as ((data_t*)((char*)devData + row*pitch))[col].

Copy this memory using cudaMemcpy2D():

cudaMemcpy2D(dest, destpitch, src, srcpitch, row_width, numrows, direction);

where destpitch, srcpitch and row_width are in bytes and indicate respectively:

• the pitch of the destination (how many bytes separate the beginning of each row)
• the pitch of the source (as above)
• the actual size in bytes of the row data (which is less than or equal to the source pitch)

Coalescing rules

Capability 1.0 and 1.1:

• the granularity is the half-warp
• a single transaction can read
  • 16 4-byte words in the same 64-byte segment
  • 16 8-byte words in the same 128-byte segment
• two transactions are used to access
  • 16 16-byte words in two consecutive 128-byte segment
• threads must access words in sequence
• if accesses cannot be coalesced, 16 transactions are issued

Capability 1.2 and 1.3:

• threads can access words randomly
• the transactions are minimized to the smallest number of transactions needed

Capability 2.0 and 2.1:

• global memory access is cached with 128-byte cache lines
• L1 cache uses the same memory banks as shared memory
• the amount of L1 cache vs shared memory can be configured

cudaFuncSetCacheConfig(kernelName, preference) where preference is one of:

• cudaFuncCachePreferShared: 48K of shared memory, 16K of L1 cache
• cudaFuncCachePreferL1: 16K of shared memory, 48K of L1 cache
• cudaFuncCachePreferNone: (default) use whatever setting the card is at

(Images courtesy of the CUDA C Programming Guide)

Shared memory and bank conflicts

Shared memory is divided into banks. 32-bit (4-byte) words are assigned consecutively to banks. The bandwidth is 32 bits per two clock cycles.

Shared memory is typically as fast as the registers. Bank conflicts (accesses to the same bank) introduce a latency.

Each half-warp issues memory requests independently. Threads in the first half cannot have bank conflicts with threads in the second half.

Broadcasting: if all threads access the same word, the data is broadcast (no bank conflicts).

Common access: 32-bit strided access (float, float2, float3, float4 etc).

Bank conflicts happen if the stride is even (e.g. float2, float4), no bank conflict happens if stride is odd (e.g. float, float3).

8-bit and 16-bit access: all accesses cause bank conflicts unless the data is interleaved.

64-bit accesses or higher: bank conflicts cannot be avoided.

Capability 2.x: 32 banks instead of 16 banks. Memory access to the same 32-bit word are broadcast (no bank conflicts for 8-bit and 16-bit access). 64-bit accesses are split into non-conflict 32-bit accesses. 128-bit accesses cause 2-way bank conflicts.

(See pictures in the programming guide.)

Maximizing instruction throughput

• prefer fast instructions over slow instructions (e.g. single instead of double precision, use instrinsic instead of general functions)
• minimize number of conditionals, minimize divergence in presence of conditionals
• reduce synchronization points and operation dependency

Devices with capability 1.x have fast 24-bit integer multiply. __mul24 can be used instead of the standard product when the result does not overflow. Devices with capability 2.x have fast 32-bit integer multiply, and __mul24 is actually slower.

Some compiler flags control the use of functions such as logarithm, exponential, and trig functions. (--use_fast_math and the booleans --ftz=, --prec-div=, --prec-sqrt= which change treatment of denormals and the precision of division and square roots).

Optimization recommendations

1. find ways to parallelize sequential code
2. minimize data transfers between the host and the device
3. adjust kernel launch configuration to maximize device utilization
4. ensure global memory accesses are coalesced
5. replace global memory accesses with shared memory accesses whenever possible
6. avoid bank conflicts in shared memory
7. avoid different execution paths within the same warp

Profiling

CUDA profiler. Hands-on experience.

An example

Smoothing an image (averaging each pixel with its immediate neighbors).

To help reduce timing fluctuations, we launch the kernel 3 times and average the time. An extra kernel launch before the timing removes the kernel loading time.

Naive approach

• launch a thread per pixel
• each thread loads the data for the corresponding pixel and the 8 neighbors
• 64x8 threads per block

Source: routines to load/save PAM files, source code

Timing on a GeForce 9600M GT: 57ms.

(Timings are for a 664x1024 RGB image).

Caching using shared memory

Threads in the same block use much of the same data. We can preload all data in shared memory and thus load each pixel data once.

• launch a thread per pixel
• each block loads all the data in shared memory
• neighbor data is then read from shared memory
• 64x8 threads per block

Source: routines to load/save PAM files, source code

Timing on a GeForce 9600M GT: 19ms.

We have a 3x speed-up. The profiler shows that we have about 6 times less loads from global memory, but about 2 times more divergent branches.

Aligning the pixel data

The profiler shows that all reads are uncoalesced (gld coalesced is 0). This is because we read ushort3 data (RGB, no alpha channel). We can force the data to be aligned optimally by padding pixel data so that it always has an even number of channels.

• launch a thread per pixel
• each thread loads the data for the corresponding pixel and the 8 neighbors
• 64x8 threads per block

Source: routines to load/save PAM files with padding, source code

Timing on a GeForce 9600M GT: 16ms.

Aligning the pixel data and caching the loads

We can still use shared memory to cache the data. However, since more memory is now used, we must use smaller blocks

• launch a thread per pixel
• each block loads all the data in shared memory
• neighbor data is then read from shared memory
• 32x8 threads per block

Source: routines to load/save PAM files with padding, source code

Timing on a GeForce 9600M GT: 13ms.

Aligning the image rows

Not all rows are properly aligned, because each row has 664 pixels. Indeed, working with the transposed image (1024x664) gives better timings: 13ms without shared memory, 12ms with shared memory.

We can align all rows properly using pitched memory allocation.

• launch a thread per pixel
• each thread loads the data for the corresponding pixel and the 8 neighbors
• 64x8 threads per block

Source: routines to load/save PAM files with padding, source code

Timing on a GeForce 9600M GT: 16ms.

Aligning rows and caching

We can combine the previous optimization with the shared memory caching. Again, we have to reduce the block size.

• launch a thread per pixel
• each block loads all the data in shared memory
• neighbor data is then read from shared memory
• 32x8 threads per block

Source: routines to load/save PAM files with padding, source code

Timing on a GeForce 9600M GT: 12ms.

A note on shared memory initialization

There are a number of possible approaches to loading data into shared memory. The one shown in the mentioned files (load central block, load borders) is not the most efficient.

Animated graph: shared memory loading pattern

Final remarks

The timings on these examples are done on a GeForce 9600M GT, which has capability 1.1 and therefore the worst possible coalescing capability. On different hardware, different strategies would be more appropriate.

Optimizing memory access on lower hardware gives a much more significant benefit than relying on shared memory for caching. On 2.0 hardware and higher, we would not try using the shared memory at all, and expoit the L1 caching instead.