Sketchy proof of the Confluence Theorem

We first define the relation  =>beta   (beta-parallel reduction).
 
Informally,  M => N  holds whenever N is obtained out of M by simulataneously reducing some (possibly none or all) of the redexes in M.


We can formally define the above relation by means of the following formal system

                     ________
Axiom             x => x


Rules
                              M => N                                     M => M'         N => N'
                        --------------------                   ------------------------------------
                          \x.M => \x.N                                           MN => M'N'        

                                            M => M'     N => N'
                                         ------------------------------
                                           (\x.M)N => M'[N'/x]

It is possible to prove that, in case a judgment like  M => N is derivable, then N is obtained out of M by simultaneously reducing a subset of its redexes.


It is possible to prove the following intuitive properties.
 
(i) If  M => N  then  M -->>  N

(ii) If  M --> N then  M => N

Notice that the viceversa of (i) does not hold, that is  M -->> N does not imply  M => N

In fact (\x.xy)(II) -->>  y   but it is not true that  (\x.xy)( II) =>  y  .
The intuitive motivation why the viceversa of (i) does not hold is that, if we beta-reduce a term P, the reduction can create a redex not present in P.

In the sequence    (\x.xy)( II) -->  (\x.xy)I --> Iy --> y
the underlined redex was not present in the starting term. It has been created by the second reduction. Such a redex cannot obviously be reduced by a parallel reduction of  (\x.xy)(II), since it does not exist yet.

It is possible to prove DP(=>), i.e. that the diamond property holds for =>:

We do not formally prove DP(=>), but we can provide the intuition underlying the proof:
it is enough to define a function (-)* that, given a term M, returns the term obtained by reducing all the redexes of M.
It is not difficult then to show that  M => N implies N => M*
DP(=>) follows now easily, since if   N' <= P => N , then  N' => P* <= N .

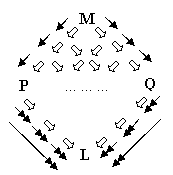
We have now all the ingredients to prove the Confluence Theorem.

Let us assume
                                       P <<---  M  --->> Q

That is                P <-- .... <-- M --> ....--> Q

By the property (ii) above we have that

                          P <= ... <= M =>...=> Q

We can now use the Diamond property for => in order to get, tile by tile , a term L such that

                         P => ... => L <=...<= Q

Now, by using property (i) above we can obtain

                          P --> ... --> L <--...<-- Q

That is  P --->>  L << --- Q