|
Uno dei problemi fondamentali che incontriamo quando vogliamo usare un sistema di calcolo per manipolare delle informazioni é quello di rappresentare le informazioni stesse all'interno del sistema. Questo problema viene risolto in informatica mediante l'adozione di opportuni codici che stabiliscono una corrispondenza tra la "informazione" significativa per il problema (l'applicazione) che si sta considerando ed una serie di simboli manipolabili dal sistema. Per esempio, i simboli manipolabili da una macchina astratta possono essere numeri interi di valore non superiore ad una soglia prefissata, quindi ogni informazione deve essere codificata sotto tale forma per poter essere trattata dal sistema. Possiamo pensare di dare una definizione "astratta" del concetto di codice, senza far riferimento a nessun esempio specifico. Poi però istanzieremo i problemi su una serie di esempi diversi per renderci conto che anche un concetto molto astratto e generale ci può aiutare molto a risolvere problemi concreti e specifici. Sia X un qualsiasi insieme (finito o infinito), che rappresenta gli oggetti o le informazioni che vogliamo trattare. Sia A un qualsiasi alfabeto finito di simboli (le 10 cifre arabe, oppure le 21 lettere dell'alfabeto italiano, oppure l'insieme dei tre colori rosso giallo e verde, non importa ...). Con A* indichiamo l'insieme di tutte le possibili sequenze (ordinate da sinistra a destra) di simboli dell'alfabeto A, di lunghezza finita, compresa la sequenza vuota (che non contiene nessun simbolo).
Definiamo una funzione iniettiva di codifica
ed una relativa funzione di decodifica tali che per ogni y appartenente ad X, decod(cod(y)) = y
L'insieme X, l'alfabeto A, e le funzioni cod e decod formano
un Codice per la rappresentazione di elementi di X.
La sequenza di simboli cod(y) corrispondente ad un qualsiasi elemento
y appartenente ad X
verrà chiamata "codifica di y" (ovvero "rappresentazione di y")
(secondo il codice considerato).
Normalmente non tutte le sequenze di simboli b appartenenti ad A*
saranno rappresentazioni di elementi appartenenti ad X.
Solitamente, anzi, in Informatica avremo a che fare con codici
a lunghezza fissa,
nei quali é predeterminato il numero di simboli che
costituiscono una codifica corretta, e tutte le altre sequenze
(che ovviamente darebbero decod(b)= errore) non vengono neanche
prese in considerazione.
Rappresentazione di numeri naturaliCominciamo quindi a trattare il caso semplice della rappresentazione dei numeri naturali 0, 1, 2, ..., ecc. Può sembrare un problema di scarsa rilevanza, visto che viene insegnato ai bambini della scuola elementare. In realtà non vogliamo verificare se ci ricordiamo le nozioni apprese alla scuola elementare, ma piuttosto provare a riflettere sul metodo seguito per arrivare a definire un codice di rappresentazione "conveniente" per un essere umano e cercare di capire in quale misura metodi analoghi ci possono portare a definire codici di rappresentazione "convenienti" per un sistema di calcolo; partiamo infatti dal presupposto che una tecnica conveniente per un bambino di 6 anni non sia necessariamente conveniente per un sistema di calcolo e viceversa. In effetti bisogna stabilire quali sono gli usi per i quali un codice di rappresentazione viene proposto. Se l'unico scopo é quello di scrivere un numero su un pezzo di carta e poi poterlo rileggere, potremmo pensare di ottimizzare la superficie di carta occupata da un simbolo, in modo da intaccare il meno possibile l'equilibrio ecologico delle foreste che ci forniscono la materia prima per produrre carta. Se invece pensiamo di utilizzare la rappresentazione scritta dei numeri per sviluppare degli algoritmi di calcolo (per esempio somma tra due numeri), allora il criterio principale diventerà quello di semplificare al massimo tale operazione, in modo da limitare per quanto possibile sia il tempo per arrivare a produrre il risultato, sia la probabilità di commettere errori di calcolo. Se vogliamo poi proporre un codice "di uso generale", ovvero usare sempre lo stesso codice per tante esigenze diverse, allora dovremo necessariamente cercare un codice di "compromesso" che non sia "troppo peggio" di altri per nessuna delle applicazioni più frequenti. Ovviamente, le considerazioni generali che facciamo qui sui codici di rappresentazione dei numeri vanno intese come esempi di problemi. La rappresentazione di numeri all'interno di un sistema di calcolo é ormai altrettanto consolidata quanto l'uso del sistema decimale posizionale con cifre arabe insegnato alle elementari, tanto é vero che esistono degli standard internazionali ormai seguiti da tutti i produttori di sistemi. Quindi nel futuro della vita professionale di un informatico nessuno verrà mai a chiedergli di inventare un nuovo codice per la rappresentazione di numeri. Tuttavia il problema si presenta abbastanza spesso per la rappresentazione di altri tipi di informazioni, per cui é importante acquisire una capacità critica e di riflessione su questa classe di problemi. Scrivere i numeri su cartaFacciamo finta di non conoscere (o di aver dimenticato) la rappresentazione decimale posizionale dei numeri a cui siamo così tanto abituati. Un'altra rappresentazione di numeri che tutti noi italiani dovremmo conoscere (ma che non usiamo quasi mai) é quella romana. Numeri Romani
Facciamo un breve ripasso di tale rappresentazione.
Viene usato un alfabeto di sette simboli: Il criterio ispiratore di tale algoritmo di codifica (che prevede una rappresentazione unica per ogni numero) é quello di minimizzare il numero di occorrenze di simboli utilizzati. Ricordiamo che il numero "due" viene rappresentato con due occorrenze del simbolo usato per rappresentare "uno" (ovvero II), ed il numero "tre" viene rappresentato da tre occorrenze del simbolo usato per rappresentare "uno" (ossia III). Per il numero cinque si sarebbe potuto utilizzare lo stesso metodo (ossia rappresentarlo con IIIII), ma questo avrebbe richiesto l'uso di cinque occorrenze, mentre l'uso del simbolo associato al cinque (ossia V) permette di rappresentare il numero con una sola occorrenza. Il modo "strano" di rappresentare il numero "quattro" (ossia IV) dando il significato di sottrazione all'ordinamento di un simbolo di valore inferiore precedente un simbolo di valore superiore é una astuzia per ridurre a due il numero di occorrenze rispetto alla ovvia rappresentazione IIII che invece ne richiederebbe quattro.
Tra i maggiori difetti (dal nostro punto di vista) della rappresentazione
romana dei numeri, vi é quello di mancanza di uniformità
dell'algoritmo per numeri di valore maggiore o uguale a quattromila, dovuta alla
mancanza di simboli unici per la rappresentazione di cinquemila, diecimila,
cinquantamila, ecc.
Questo ci costringe, per esempio a rappresentare il numero cinquantamila mediante
cinquanta occorrenze del simbolo M, un vero attentato alle capacità cognitive
di qualunque persona umana: chi riuscirebbe mai "a colpo d'occhio"
a riconoscere se nella seguente rappresentazione ci sono cinquanta o quarantanove
o cinquantuno occorrenze? Tra i maggiori pregi della rappresentazione romana, possiamo invece notare la facilità con coi vengono rappresentati numeri "arrotondati" ai numeri fondamentali rispetto a numeri arbitrari, indipendentemente dal loro valore. Questo in un certo senso corrisponde alle nostre capacità cognitive: per noi é sicuramente più facile ricordare numeri come cinquecento, mille, millecinquecento (in romano D, M, MD) piuttosto che quattrocentoquarantotto, milleventiquattro, milleduecentottantuno (in romano CDXLVIII, MXXIV, MCCLXXXI). In oltre ricordare il numero mille non ci comporta difficoltà superiori rispetto al numero cento, o dieci. Provate a pronunciare tali numeri ad alta voce per convincervi che anche a livello verbale noi diamo la preferenza di una maggior sinteticità ai numeri arrotondati alle potenze di dieci. Tale corrispondenza non esiste invece nella rappresentazione decimale a cui siamo abituati da tanto tempo (448 e 500 sono entrambi rappresentati su tre cifre, mentre 1000 é rappresentato su quattro cifre, quindi implica una maggiore complessità di scrittura). Numeri decimali posizionaliÉ inutile ricordare come rappresentiamo usualmente i numeri. Siamo talmente abituati a questa rappresentazione che spesso confondiamo la rappresentazione decimale posizionale di un numero con il "numero stesso" (ossia col concetto matematico di numero). Qualitativamente, il sistema decimale posizionale ha un vantaggio fondamentale rispetto al sistema romano per la rappresentazione di numeri molto grandi: il numero di cifre (ovvero di occorrenze di simboli dell'alfabeto, secondo la nostra terminologia informatica) cresce in modo logaritmico con il valore del numero da rappresentare, anziché in modo lineare. Uno svantaggio é quello di richiedere un numero di occorrenze di simboli identico per numeri dello stesso ordine di grandezza, indipendentemente dalla "regolarità" del numero che ci può facilitare o meno lo sforzo di memorizzazione. Operazioni aritmetiche e codificaNormalmente gli informatici non sono interessati solo agli aspetti di memorizzazione e lettura di informazioni, ma anche alla loro manipolazione. Nel caso di numeri, i tipi più semplici di manipolazione che possiamo incontrare sono le operazioni aritmetiche tra coppie di numeri. Ovviamente le operazioni aritmetiche sono definite dal punto di vista matematico su dei "numeri astratti" indipendentemente dal fatto che questi vengano rappresentati con un codice piuttosto che un altro. Tuttavia quando vogliamo definire un algoritmo meccanizzabile per effettuare per esempio la somma, allora questo algoritmo deve operare su una rappresentazione concreta dei numerali che vogliamo sommare. Il punto che vogliamo evidenziare qui é che la complessità dell'algoritmo di manipolazione dei dati (nel nostro esempio la somma) dipende dalla rappresentazione che stiamo utilizzando. Cambiando la rappresentazione possiamo ottenere algoritmi di manipolazione più o meno semplici e più o meno efficienti. Per esempio, un algoritmo di somma tra due numeri che operasse sulla rappresentazione romana di numeri naturali risulterebbe estremamente complesso da concepire (oltre che inefficiente da eseguire). Non per nulla gli antichi inventarono l'abaco (pallottoliere) come metodo alternativo di rappresentazione dei numeri in grado di supportare un semplice ed efficace algoritmo di somma e di sottrazione. Quindi, se adottassimo ancora il metodo romano di scrittura dei numeri, dovremmo prima decodificare il numero trasformandolo in una equivalente rappresentazione su un abaco, poi effettuare l'operazione aritmetica richiesta, e infine ricodificare il risultato nel codice usato per la scrittura. Il codice decimale posizionale, invece, ci consente di applicare un algoritmo di somma molto semplice ed efficace (di complessità logaritmica nel valore dei numeri trattati, così come il numero di cifre usate per la rappresentazione) che opera direttamente sulla codifica del numero producendo la codifica del risultato. Mediante l'uso della tavola Pitagorica possiamo in modo analogo sviluppare un algoritmo per la moltiplicazione. Algoritmi più o meno complessi operanti direttamente sulla rappresentazione sono in oltre conosciuti (e studiati a scuola) per la realizzazione delle operazioni di divisione, calcolo della radice quadrata, ecc. La disponibilità di questi algoritmi ha sicuramente contribuito in maniera decisiva alla "scelta" di questo metodo di rappresentazione rispetto alle tante altre alternative che uno potrebbe immaginare di adottare. Tornando a considerare il problema di rappresentazione di numeri all'interno di un sistema di calcolo, la considerazione sulla possibilità di supportare efficacemente algoritmi di manipolazione diventa il criterio principale di scelta per un codice piuttosto di un altro, oltre alle caratteristiche di concisione della rappresentazione. Codici N-ari posizionaliI vantaggi del sistema di rappresentazione decimale posizionale non derivano dal fatto di aver scelto un alfabeto di dieci simboli ("0", "1", "2", ... "9"), ma piuttosto dal modo di usare ed interpretare questi simboli per costruire le rappresentazioni dei numeri. Possiamo quindi generalizzare questo codice al caso di N (non necessariamente uguale a dieci) simboli diversi, mantenendo invariate tutte le altre regole di codifica. Nel caso di alfabeto di due simboli (per esempio "0" e "1"), otteniamo la famigerata rappresentazione binaria, incubo di ogni informatico neofita. La i-esima cifra da destra verso sinistra rappresenta il coefficiente moltiplicativo della i-esima potenza di due (anziché di dieci) che compone il numero. Possiamo applicare tranquillamente gli algoritmi noti per la rappresentazione decimale di somma, differenza, moltiplicazione, divisione, ecc. alla rappresentazione binaria, semplicemente ricordandosi che "il riporto" viene generato al superamento della cifra "1" anziché "9". Il vantaggio di questa rappresentazione dal punto di vista informatico deriva da vincoli di tipo realizzativo dei dispositivi elettronici: dispositivi in grado di operare distinzioni e manipolazioni di due soli simboli (o meglio, grandezze elettromagnetiche) sono più facili da realizzare e meno costosi di dispositivi in grado di operare su un numero maggiore di simboli. Ponendo N=8 oppure N=16 si ottengono i sistemi di numerazione ottale ed esadecimale. L'interesse informatico per questi codici deriva da una loro sostanziale omogeneità col sistema binario accoppiata ad una maggior concisione (in termini di numero di cifre utilizzate per rappresentare un determinato valore). In effetti, la conversione da binario ad ottale o esadecimale, e viceversa risulta essere particolarmente semplificata dal fatto che in entrambi i casi il numero di simboli é una potenza di due. Nel caso della rappresentazione ottale, per esempio, si può stabilire una corrispondenza tra terne di simboli della rappresentazione binaria e singoli simboli della rappresentazione ottale dello stesso numero; in questo senso, la rappresentazione ottale può essere vista come una pura e semplice abbreviazione della rappresentazione binaria, che sostituisce ad ogni terna di cifre binarie consecutive una sola cifra ottale.
Algoritmo di codifica per divisioni successive. (F.B.)Il seguente algoritmo in pseudocodice permette di ottenere, dato un numero naturale n, la sua rappresentazione posizionale in base B.In pratica, si divide il numero n per B, il resto della divisione sara' la cifra meno significativa (quella piu' a destra) della rappresentazione posizionale. Si prosegue prendendo il quoziente della divisione e si divide per B. Il resto sara' la seconda cifra. Si prosegue cosi', fino ad ottenere quoziente uguale a 0. Il resto di quest'ultima divisione sara' la cifra piu' significativa (quella piu' a sinistra). input n val := n i:= 0 REPEAT quoz := val val := quoz div B ci := quoz mod B i := i+1 UNTIL (quoz < B)Dimostriamo a grandi linee perche' quest'algoritmo funziona. Dobbiamo trovare quelle cifre
cp-1cp-2....c2c1c0
tali che
n = ∑ ciBi i=0 Quindi la cifra meno significativa sarebbe proprio il resto della divisione per B. Il quoziente di questa divisone e' ∑i=1 p-1 ciBi-1. Tale quoziente lo possiamo anche vedere come B*(∑i=2 p-1 ciBi-2) + c1. E c1 e' il resto dell'ulteriore divisione per B. Iterando questa procedura otteniamo tutte le cifre della nostra rappresentazione.
Conversione di rappresentazioni tra basi una potenza dell'altra. (F.B.)Per semplicita' consideriamo la rappresentazione posizionale binaria (si puo' comunque generalizzare facilmente a qualsiasi base).E' consuetudine, per motivi di compattezza della rappresentazione, rappresentare il contenuto di un byte di memoria (quindi una stringa di otto cifre binarie) con una stringa di due cifre esadecimali (precedute dai caratteri "0x" che stanno ad indicare che cio' che segue e' appunto un numero in esadecimale). Le due cifre esadecimali corrispondono alla rappresentazione del numero naturale corrispondente agli otto bit, se questi fossero interpretati come la rappresentazione in binario di un numero naturale. Ecco che il byte 00101101 (che corrisponde a 45 in binario) viene rappresentato da 0x2D (che e' appunto la rappresentazione esadecimale di 45) Viene naturale chiedersi il motivo di cio'. Perche' non utilizzare, per esempio, la rappresentazione decimale? o quella in base venti? C'e' in realta' un motivo preciso per questa scelta. Infatti la conversione tra una rappresentazione in base 2 ed una in una qualsiasi base che sia una potenza di 2 si puo' ottenere con un semplicissimo algoritmo che ora descriviamo per la conversione da rappresentazione in base 2 a base 24. Prendiamo la stringa 00101101. Le cifre della rappresentazione esadecimale sappiamo che corrispondono ai numeri da 0 a 15. Con quante cifre binarie si possono rappresentare i numeri da 0 a 15? con quattro cifre. Dividiamo quindi la stringa in blocchi da 4 bit (0010 e 1101), e per ogni blocco consideriamo la cifra esadecimale corrispondente al numero rappresentato dai vari blocchi. 0010 rappresenta il numero 2, che corrisponde alla cifra esadecimale '2'. mentre il blocco 1101 rappresenta il numero 13, che corrisponde alla cifra esadecimale 'D'. Guarda caso (che non e' un caso) la stringa esadecimale 2D e' proprio la conversione in esadecimale del numero rappresentato in binario da 00101101. Vediamo perche' cio' funziona: Prendiamo una sequenza di 8 cifre binarie:
c7c6c5c4c3c2c1c0
Questa corrisponde al numero
c7*27+c6*26+c5*25+c424+c3*23+c222+c1*21+c0*20
e quindi, facendo semplici trasformazioni, a
(c7*23+c6*22+c5*21+c420)*24+(c3*23+c222+c1*21+c0*20)*1
e cioe'
(c7*23+c6*22+c5*21+c420)*161+(c3*23+c222+c1*21+c0*20)*160 [**]
dove (c7*23+c6*22+c5*21+c420)
non e' niente altro che il numero rappresentato dal primo blocco di 4 bit (che possiamo rappresentare con una cifra esadecimale, mettiamo e1)
mentre (c3*23+c222+c1*21+c0*20) il numero rappresentato dal secondo blocco di 4 bit (che possiamo rappresentare con una cifra esadecimale, mettiamo e0).
Ecco che che l'espressione [**] si puo' esprimere anche come
e1*161+e0*160
E quindi il numero rappresentato in binario da 00101101
e' rappresentato in esadecimale da e1e0 (o con la
notazione 0xe1e0).
E' facile vedere che questo ragionamento si puo' estendere a qualsiasi sequenza binaria, non solo 8 cifre. Inoltre si puo' considerare qualsiasi base che sia una potenza di 2 (per rappresentare i byte conviene pero' l'esadecimale, poiche' un byte e' composto da due blocchi di quattro bit). Notare come sia altrettanto facile passare dalla rappresentazione esadecimale a quella binaria: basta "espandere" in binario le singole cifre del numero in esadecimale che si intende convertire in binario. Per esempio, la conversione in binario di 0xB3 si ottiene prendendo i 4 bit che rappresentano in binario il numero rappresentato da 'B', cioe' 1011, poiche' 'B' rappresenta il numero 11) e facendoli seguire dai 4 bit che rappresentano '3'. La conversione in binario di 0xB3 e' infatti 10110011. La conversione in binario di 0xA7B e' 101001111011 (1010 e' A, 0111 e' 7 e 1011 e' B). La conversione in binario del numero ottale 755 e' invece 111101101 (111 e' 7, 101 e' 5 e 101 e' 5). La dimostrazione della correttezza di tale procedimento e' simile a quella della conversione da binario ad esadecimale ed e' lasciata come esercizio. Codici a lunghezza fissaSu carta noi siamo abituati ad applicare un principio di economicità della rappresentazione che ci porta a definire la regola: "non si scrive zero come cifra più a sinistra". In questo modo, oltre a risparmiare carta, otteniamo anche una rappresentazione unica per ogni numero. In mancanza di questa regola noi potremmo scrivere un certo numero (per esempio cinquantesette) in un numero potenzialmente infinito di modi diversi, semplicemente aggiungendo un numero arbitrario di cifre "0" a sinistra di una rappresentazione scritta dello stesso numero (ossia: 57, 057, 0057, 00057, ecc.). D'altra parte, questa abitudine di scrivere numeri in forma minima corrisponde all'uso di un codice a lunghezza variabile, in cui numeri di valore diverso richiedono un numero di cifre diverso per la rappresentazione. Di solito questa caratteristica del codice non ci crea problemi, anche perché di solito non scriviamo numeri di valore molto grande. Tuttavia, se vogliamo applicare l'algoritmo di addizione, uno dei requisiti é quello di poter allineare le rappresentazioni degli addendi a destra, in modo da porre sulla stessa verticale le cifre che rappresentano le unità, le decine, ecc. Se per esempio vogliamo sommare una lunga sequenza di numeri, nel momento in cui scriviamo il primo numero della lista dobbiamo assicuraci di riservare sulla sinistra uno spazio sufficiente per la scrittura di tutte le cifre del più grande degli addendi. Una volta scritto il primo addendo, la distanza dal margine sinistro del foglio della sua cifra più a destra determina implicitamente il numero massimo di cifre che potremo utilizzare per scrivere un numero allineato per una operazione di somma (almeno se ammettiamo di scrivere tutte le cifre della stessa dimensione). Questa considerazione ci mostra la necessità di stabilire un massimo valore rappresentabile quando vogliamo prefissare delle risorse da dedicare alla realizzazione di un algoritmo (per esempio una risma di fogli in formato A4). Volendo usare un sistema di calcolo per la realizzazione di algoritmi dobbiamo preoccuparci di definire a priori delle risorse dedicate alla rappresentazione dei dati. Il modo più semplice per arrivare a gestire queste risorse nel caso della rappresentazione di numeri naturali é quello di definire a priori un valore massimo rappresentabile per ogni numero (a cui corrisponde un numero massimo di cifre impiegate per la rappresentazione), con l'accortezza di usare un valore massimo sufficientemente grande da poter trattare tutti (o quasi) i casi di rilevanza pratica, ma sufficientemente piccolo da non sprecare inutilmente risorse costose del sistema. Una volta determinato il massimo valore rappresentabile, questo determina anche il numero di cifre (decimali, binarie, ottali, o altro) da usare per la sua rappresentazione. Un codice viene detto a lunghezza fissa quando viene sempre usato lo stesso numero di cifre per la rappresentazione di qualunque valore. Ovviamente il numero di cifre da usare é in questo caso il numero minimo di cifre per la rappresentazione del massimo valore predeterminato. Per esempio, se decidessimo di trattare numeri non superiori a 9999, potremmo usare una rappresentazione decimale posizionale fissa a 4 cifre. In tal caso il numero cinquantasette verrebbe rappresentato (in modo unico) come "0057". Codici a lunghezza variabileQuando consideriamo il sistema di rappresentazione N-ario posizionale, abbiamo detto facciamo uso di un alfabeto di N simboli. Questo é vero nel caso di rappresentazioni a lunghezza fissa ma falso nel caso di rappresentazioni a lunghezza variabile. In realtà se usiamo la versione usuale della rappresentazione (senza zeri come cifra più a sinistra, quindi in rappresentazione non fissa e minimale) noi facciamo implicitamente uso di un N+1-esimo "simbolo", normalmente lo spazio bianco: l'assenza di ulteriori cifre più a sinistra (e quindi lo spazio bianco invece di una cifra) indica dove termina la rappresentazione del numero. Normalmente, infatti, interpretiamo la presenza di uno spazio bianco a sinistra di una cifra come l'indicazione che quella cifra é la cifra più significativa e che non ce ne saranno altre più a sinistra. In mancanza di questa informazione associata allo spazio vuoto, noi potremmo pensare che la cifra precedente sia scritta "un po' più a sinistra di dove abbiamo guardato sin ora", e non potremmo mai terminare la lettura di un numero. Solo il raggiungimento del margine del foglio ci darebbe la certezza che non ci sono altre cifre più a sinistra, ma se ammettiamo che esista sempre un margine a sinistra del foglio alla nostra portata visiva implicitamente poniamo un vincolo al numero massimo di cifre rappresentabili. Per risolvere questa contraddizione non ci resta che prendere atto che senza un N+1-esimo (nel nostro esempio lo spazio vuoto) non possiamo scrivere un valore in rappresentazione posizionale base N con numero arbitrario di cifre. Da qui deriva la necessità concettuale (dal punto di vista informatico) di delimitare la cifra più a sinistra della rappresentazione nel caso di codici di rappresentazione a lunghezza variabile. In informatica si parla quindi di codici a lunghezza variabile nei casi in cui si prevede l'uso di un numero di cifre variabile in funzione del valore da rappresentare, ma tali per cui nell'alfabeto esistono dei simboli espliciti usati per individuare la terminazione della rappresentazione. Per esempio, la normale rappresentazione decimale con numero di cifre variabile potrebbe essere facilmente trasformata in un codice ad espansione utilizzabile in un sistema di calcolo mediante la seguente modifica: usare un alfabeto ad undici simboli che includa oltre alle dieci cifre anche il carattere "#"; la cifra più a sinistra di una rappresentazione é sempre "#"; la cifra "0" non può mai seguire la cifra "#", tranne nel caso in cui sia la cifra più a destra. Usando questa regola modificata, ogni numero avrebbe ancora una rappresentazione unica. I numeri zero, uno, due, cinquantasette sarebbero rappresentati come "#0", "#1", "#2", "#57". Leggendo le cifre da destra verso sinistra, se troviamo una delle dieci cifre arabe allora sappiamo di dover continuare la lettura della rappresentazione incontrando almeno un'altra cifra verso sinistra; se invece incontriamo il simbolo di terminazione, allora sappiamo che la codifica non contiene altre cifre più a sinistra (e quindi possiamo interrompere la lettura del numero). Un altro esempio più concreto può essere quello della codifica di una testo su un supporto informatico. Ciascun carattere (lettera alfabetica maiuscola o minuscola, cifre araba, segno di punteggiatura, spazio vuoto, ecc.) viene rappresentato come un simbolo di un alfabeto predefinito. Per esempio si può ricorrere al codice ASCII per definire un alfabeto di 128 simboli di base adatti allo scopo. In termini astratti possiamo quindi trattare una qualunque sequenza di questi caratteri come una rappresentazione in base 128. Per poter riconoscere la fine di un testo dovremo però riservare uno dei 128 simboli alla rappresentazione della informazione "fine del testo". Solo 127 caratteri ASCII resteranno quindi disponibili per la codifica del testo stesso. Normalmente nel caso di sistemi Unix e/o linguaggio di programmazione C il simbolo 0 (chiamato "nul") é riservato a questo scopo.
Codici a espansioneNel caso dei codici a lunghezza variabile appena discusso "sprechiamo" uno dei simboli dell'alfabeto per codificare la fine delle cifre della codifica. Esistono delle alternative per ottenere un codice ad espansione a partire da un codice a lunghezza fissa senza modificare l'alfabeto. Consideriamo per esempio una rappresentazione binaria di numeri, e supponiamo di raggruppare un certo numero di cifre in "quanti" prefissati. Potremmo per esempio supporre di partire da una rappresentazione fissa su 5 cifre binarie (massimo numero rappresentabile 31), e pensare poi di aggiungere altri "gruppi di cifre" alla rappresentazione di base per rappresentare numeri superiori (non rappresentabili col numero di cifre della rappresentazione di partenza). Vediamo una serie di esempi. Esempio di codice a formati multipli predefinitiSupponiamo di voler definire un codice che preveda l'uso di uno tra 4 formati di rappresentazione: uno su 4 cifre binarie, un secondo formato su 7 bit, un terzo formato su 10 bit ed un ultimo su 16 bit. I 4 formati di rappresentazione devono essere distinguibili l'uno dall'altro, quindi possiamo pensare di numerarli da 0 a 3, ed inserire il numero del formato nelle prime due cifre della rappresentazione binaria. Il primo formato sarà quindi costituito sempre dalle prime due cifre "00", seguite da altre due cifre binarie; il secondo sarà costituito sempre dalle prime due cifre "01", seguite da altre 5 cifre binarie; il terzo sarà costituito sempre da "10" seguito da altre 8 cifre binarie; l'ultimo formato sarà costituito sempre da "11" seguito da altre 14 cifre binarie. Possiamo quindi pensare di usare questo codice per rappresentare i numeri da 0 a 3 usando il primo formato su 4 cifre (0000 ÷ 0011), i numeri da 4 a 35 usando il secondo formato (0100000 ÷ 0111111), i numeri da 36 a 291 usando il terzo formato (1000000000 ÷ 1000000000) ed i numeri da 292 a 16675 usando il terzo formato (1100000000000000 ÷ 1111111111111111). Numeri piccoli verrebbero quindi rappresentati con un numero di cifre inferiore, numeri grandi con un numero di cifre superiore. Leggendo le prime due cifre a sinistra di qualsiasi rappresentazione si risale al formato usato, e quindi si capisce quante altre cifre devono essere lette prima di "arrivare alla fine" della rappresentazione stessa. Esempio di codice a espansione con cifra di espansioneConsideriamo un caso analogo al precedente, nel quale vogliamo usare 4 possibili formati rispettivamente su 4, 7, 10 e 16 bit. Rispetto al caso precedente cambiamo la codifica del formato usato. Il formato a 4 bit viene caratterizzato da una prima cifra al valore 0, seguita da altre tre cifre binarie "utili"; il formato a 7 bit viene caratterizzato da una prima coppia di cifre al valore costante "10", seguita da altre 5 cifre binarie "utili"; il formato a 10 bit conterrà sempre le prime tre cifre "110", seguite da altre 7 cifre; il formato a 16 bit sarà costituito sempre dalle prime tre cifre "111", seguite da altre 13 cifre binarie. Possiamo quindi usare questo codice per rappresentare i numeri da 0 a 7 con il formato a 4 bit (0000 ÷ 0111), i numeri da 8 a 39 con il formato a 7 bit (1000000 ÷ 1011111), i numeri da 40 a 167 con il formato a 10 bit (1100000000 ÷ 1101111111) ed i numeri da 168 a 8359 con il formato a 16 bit (1110000000000000 ÷ 1111111111111111). Notare come, rispetto all'esempio precedente, aumenta la capacità di codificare numeri piccoli con i formati più piccoli, mentre diminuisce la capacità di rappresentare numeri grandi con i formati a numero di bit superiore. Esempio di codice a espansione con configurazione di espansioneConsideriamo nuovamente un codice ad espansione sui 4 formati di 4, 7, 10 e 16 bit, e "proviamo" un terzo modo di codificare il passaggio da un formato ad un altro. Questa volta minimizziamo lo spreco di configurazioni dedicate al riconoscimento del formato per il formato a 4 bit, riservando una sola configurazione a rappresentare l'informazione "il formato non é quello a 4 bit". Possiamo per esempio associare la sequenza di quattro cifre 1 (ossia "1111") per rappresentare l'espansione. Rimarranno quindi 15 codifiche diverse "utili" per la rappresentazione dei numeri da 0 a 14 usando il formato a 4 bit. Leggendo qualunque combinazione diversa da "1111" nelle prime quattro cifre sapremo contemporaneamente sia il valore del numero, sia che questo era stato codificato col formato a 4 bit. Leggendo invece "1111" nelle prime quattro cifre, sapremo solo che il valore é stato codificato usando uno degli altri 3 formati. In modo analogo potremo riservare una delle 8 codifiche del formato a 7 bit (per esempio "1111111") per rappresentare l'informazione "é stato usato un formato con numero di bit maggiore di 7", e lasciare quindi le rimanenti 7 codifiche su 7 bit (1111000 ÷ 1111110) per la rappresentazione dei numeri da 15 a 21. Procedendo nello stesso modo si può riservare una delle 8 codifiche a 10 bit (per esempio "1111111111") per rappresentare la condizione "é stato usato il formato a 16 bit", e sfruttare le rimanenti 7 codifiche su 10 bit per rappresentare i numeri da 22 a 28 (1111111000 ÷ 1111111110). Infine, potremo usare tutte e 64 le configurazioni del formato a 16 bit per rappresentare i numeri da 29 a 92 (1111111111000000 ÷ 1111111111111111).
Confrontato coi metodi di espansione precedentemente illustrati, questo metodo
accentua ulteriormente le caratteristiche di poter rappresentare un numero
relativamente elevato di numeri piccoli col formato contenente il numero di
cifre binarie inferiori, ma pagando questo vantaggio con l'inefficienza di
rappresentazione dei numeri più grandi su formati di dimensione
maggiore.
A seconda del tipo di applicazione potranno essere convenienti tecniche diverse
di rappresentazione dell'espansione del formato.
Puo' risultare molto utile utilizzare codici ad espansione per codificare
i codici operativi delle istruzioni di un linguaggio macchina. La codifica di codici operativi in istruzioni con numero di bit variabile per gli argomenti la studierete nel corso di Architettura degli Elaboratori, nella sezione 2.13 del testo di Hamacher et al.
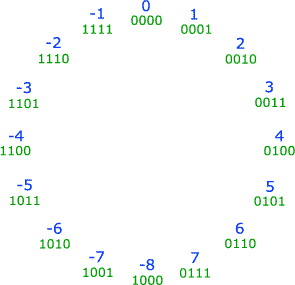
Vogliamo determinare un codice a lunghezza fissa per i numeri interi. Ne esistono molti, ma il piu' comune e' quello in complemento alla base (detto complemento a due nel caso di rappresentazione in base due). Tale codice ha molti vantaggi, tra cui: rappresentazione unica dello zero, facilita' di identificazione del segno del numero rappresentato, semplicita' dell'algoritmo per la somma e di quello per la moltiplicazione.
Indicheremo con B la base e con p il numero di posizioni che intendiamo
utilizzare per la nostra rappresentazione a lunghezza fissa.
Se B=2 e p=4 abbiamo a disposizione 16 configurazioni (indicate in verde),
che possiamo disporre su di una circonferenza in modo da fornire un'idea intuitiva di
come funziona la codifica dei numeri interi (indicati in blu) in complemento a due.
Formalmente, la funzione codZcB e' definita come segue: codZcB(r) = codNB(r) se r≥0 codZcB(r) = codNB(Bp-|r|) se r <0
E' facile notare come, volendo rappresentare tanti numeri positivi quanti numeri negativi (e scegliendo di rappresentare un numero negativo in piu' rispetto ai positivi nel caso Bp-1 sia dispari), l'intervallo di rappresentabilita' sia Quando B=2 l'intervallo di rappresentabilita' sara' quindi Potremmo in realta' anche decidere di rappresentare molti piu' positivi che negativi o viceversa, ma questa scelta dell'intervallo di rappresentabilita' possiede il grande vantaggio di permettere di determinare facilmente il segno di un numero intero data la sua rappresentazione in complemento a due:
il numero rappresentato e' negativo se e solo se il bit piu' a sinistra e' 1.
E' semplice inoltre determinare la rappresentazione dell'opposto di
un numero r data la rappresentazione di r. Per B=2 tale operazione consiste semplicemente
nel complementare (0 diventa 1 ed 1 diventa 0) tutte le cifre della rappresentazione
di r e poi sommare 1.
codZc2(-r) = dp-1...d1d0
Per far cio' cominciamo con l'osservare che la seguente equazione e' valida:
∑i=0 p-1 ci2i +
∑i=0 p-1 c'i2i = 2p-1
(poiche' con l'algoritmo di somma otteniamo una sequenza di 1 lunga p, corrispondente appunto al numero 2p-1).Da questa equazione, spostando semplicemente alcuni termini, otteniamo la seguente equazione, che utilizzeremo tra poco
∑i=0 p-1 c'i2i +1 =
2p - ∑i=0 p-1 ci2i (#)
Distinguiamo ora i due casi: r>0 e r<0 (il caso r=0 e' semplice)
codZc2(-r) = codN2(2p-|r|) =
(poiche', se r≥0, sappiamo che codZc2(r) = codN2(r) = cp-1...c1c0 e quindi che r = ∑i=0 p-1 ci2i)
= codN2(2p- ∑i=0 p-1 ci2i ) =
(usando l'equazione (#) )
= codN2(∑i=0 p-1 c'i2i +1) =
(usando l'equazione ($) )
codN2(∑i=0 p-1 di2i) =
dp-1...d1d0 Che e' appunto quel che volevamo. Se invece r<0, allora -r>0. Quindi, per definizione abbiamo che
codZc2(-r) = codN2(-r) = codN2(|r|) =
(poiche' cp-1...c1c0 = codZc2(r) =
codN2(2p - |r| ) e quindi
2p - |r| = ∑i=0 p-1 ci2i.
Da cui abbiamo che |r| = 2p -∑i=0 p-1 ci2i)
= codN2(2p - ( ∑i=0 p-1 ci2i)) =
(usando la (#) e la ($))
codN2(∑i=0 p-1 di2i) =
dp-1...d1d0 Che e' appunto quel che volevamo. Una importante proprieta' della rappresentazione dei numeri interi in complemento alla base e' che
L'affermazione [*] significa che per eseguire la somma di due interi rappresentati in complemento a due
possiamo utilizzare il normale algoritmo di somma sulle loro rappresentazioni, senza tener conto se i numeri rappresentati siano positivi o negativi. Significa quindi anche che se vogliamo eseguire
una sottrazione basta prima calcolare l'opposto del numero da sottrarre e poi eseguire un'addizione.
Ovviamente l'affermazione [*] e' corretta solo se la somma dei numeri che
sono rappresentati in complemento a due appartiene all'intervallo di rappresentabilita'.
In caso contrario si ottiene un risultato completamente errato (si parla di overflow se
la somma e' maggiore del limite superiore dell'intervallo di rappresentabilita';
underflow se la somma e' minore del limite inferiore). Dimostriamo l'affermazione [*] per casi.
Iniziamo a dimostrare la [*] per il caso X - Y con Y > X. = codNB(Bp - (Y - X)) = = codZcB(X - Y). Consideriamo ora il caso X - Y con Y ≤ X. = codNB(Bp + (X - Y)) =
Lasciamo come esercizio la dimostrazione dell'affermazione [*] per i casi -X-Y e X+Y Altro interessante esercizio e' dimostrare che, se Un procedimento analogo funziona anche in base B (si estendono le cifre con 0 se il numero rappresentato e' positivo e con B-1 se e' negativo)
Nella rappresentazione in complemento a 2 e' facile stabilire quando l'algoritmo di somma
e' stato applicato alle rappresentazioni di due numeri interi r1 ed r2
tali che r1+r2 non appartiene all'intervallo di rappresentazione.
E' facile cioe' stabilire quando ci sia stato supero di capacita' (overflow o underflow):
basta controllare i riporti ottenuti dalla somma delle cifre in posizione p-1 e p. Se questi riporti sono diversi c'e' stato
supero. Questa proprieta' non e' vera in generale per la rappresentazione in complemento
ad una base B diversa da 2.
Anche per quanto riguarda l'operazione di moltiplicazione, possiamo utilizzare sulla rappresentazione in complemento a due i normali algoritmi che lavorano sulla rappresentazione posizionale dei naturali ottenendo comunque risultati corretti (se ovviamente non abbiamo supero di capacita'). Si puo' dimostrare infatti che Come per [*], e' possibile dimostrare l'affermazione [**] per casi. (quello che segue si puo' anche evitare di farlo)
Dimostriamo il caso X*(-Y). = codNB((X*Bp) - (Y * X)) = = codZcB(X * (-Y)).
|