Fondamenti di Informatica, 23 Settembre 2014
Non e' ammesso l'uso di alcun testo, appunti, calcolatrici o
qualsivoglia app per smartphone. Le risposte vanno scritte nel foglio di bella copia. Si
raccomanda la massima SINTETICITA'. L'eccessiva verbosita' verra'
considerata negativamente.
Occorre essersi prenotati sul portale studenti del nostro
ateneo. Se cio' non e' stato fatto, comunicatelo immediatamente
al docente o all'assistente in aula.
I risultati
verranno indicati nella pagina web del corso.
Date ed orari degli orali, sul Forum.
Esercizio 1
(a)
Descrivere i principi di Induzione sui naturali, di Induzione Completa e di Induzione Ben-Fondata.
(b)
In quale punto della dimostrazione del Lemma di Deduzione di Herbrand viene utilizzata l'Induzione, e come?
(c)
Si consideri il seguente automa.
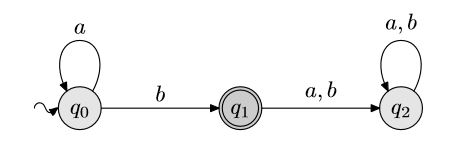
e il seguente linguaggio {an b | n≥0}.
Supponiamo di aver gia' dimostrato che le stringhe
della forma anb sono
riconosciute dall'automa.
Completare la dimostrazione che il linguaggio {an b | n≥0} coincide con il linguaggio
riconosciuto dall'automa, dimostrando formalmente per induzione che
le stringhe riconosciute dall'automa sono della forma anb.
Utilizzare il concetto di funzione di transizione δ e di
funzione
δ.
Si consideri che la funzione δ
puo' essere definita anche nel seguente modo:
δ(q,ε) = q
δ(q,ax) = δ(δ(q,a),x)
Esercizio 2
(a)
Cosa si intende per Modello Computazionale?
Descrivere brevemente, ma formalmente, il Modello Computazionale del λ-calcolo.
(b)
La funzione "incremento di uno" viene rappresentata nel λ-calcolo
con il termine λn.λf.λx.nf(fx) mentre il numero
0 viene rappresentato da λg.λy.y
Calcolare nel λ-calcolo il valore che si ottiene incrementando di uno il numero zero.
(c)
Nel modello computazionale delle funzioni parziali ricorsive,
si supponga di aver gia' definito la funzione moltiplicazione (mult).
Cosa calcola la funzione g definita nel modo seguente?
i(z,t,v) = mult( P32(z,t,v), P33(z,t,v) )
g(0,x) = C11(x)
g(y+1,x) = i(y, g(y,x), x)
Giustificare brevemente la risposta.
Esercizio 3
Fornire la rappresentazione in base ventisette
del numero rappresentato in base tre dalla seguente
sequenza di cifre: 210002102
Giustificare la risposta nel modo piu' completo
possibile.