Non e' ammesso l'uso di alcun testo, appunti, calcolatrici o qualsivoglia app per smartphone. Le risposte vanno scritte nel foglio di bella copia. Si raccomanda la massima SINTETICITA'. L'eccessiva verbosita' verra' considerata negativamente.

Occorre essersi prenotati sul portale studenti del nostro ateneo. Se cio' non e' stato fatto, comunicatelo immediatamente al docente o all'assistente in aula.

I risultati verranno indicati nella pagina web del corso. Date ed orari degli orali, sul Forum.

Esercizio 1
(a) Definire l'insieme dei λ-termini e descrivere brevemente le differenze tra la programmazione funzionale e quella imperativa.

(b) Definire formalmente la nozione di sostituzione ed effettuare la seguente sostituzione

((λy.xy)(λz.y(λy.x)))[xyz/x]

Giustificare la risposta

(c) Fornire il λ-termine che rappresenta l'operatore booleano NOT, sapendo che l'operatore IF_THEN_ELSE si rappresenta con λz.z, il valore TRUE con λx.λy.x e il valore FALSE con λx.λy.y
Giustificare la risposta

---

Esercizio 2
(a) Si consideri un sistema formale D. Fornire le definizioni di Consistenza, Insieme delle conseguenze di un insieme di fbf, Consistenza di un insieme di fbf, Teoria e Teoria pura.

(b) Nella logica dei predicati del primo ordine (calcolo dei predicati), si specifichi una segnatura Σ, una struttura A_Σ e la formula ben formata vere in A_Σ, corrispondente alla seguente affermazione:

Tutti i conoscenti comuni a Mario e ad Antonio sono italiani, ma Mario ha anche conoscenti francesi.

(c) Si consideri la logica dei predicati in deduzione naturale con uguaglianza.
Fornire una dimostrazione di

pippo=giuseppe |- ∀ x.(cugino(x,pippo) → cugino(x,giuseppe))

Ricordiamo che le due regole per l'uguaglianza in deduzione naturale che sono utili per la dimostrazione sono le seguenti:

-------
x = x

x₁ = y₁ ... x_n = y_n
-------------------------------------------------
A[x/z] → A[y/z]

Dove A e' un qualsiasi simbolo di predicato n-ario. Inoltre con la notazione x indichiamo una sequenza x₁....x_n di variabili.

---

Esercizio 3
Dimostrare formalmente che il linguaggio {aⁿ b | n≥0} coincide con il linguaggio riconosciuto dall'automa

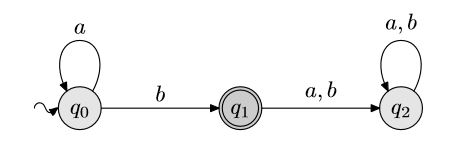
Utilizzare il concetto di funzione di transizione δ e di funzione δ.
Si consideri che la funzione δ, puo' essere definita anche nel seguente modo:
δ(q,ε) = q
δ(q,ax) = δ(δ(q,a),x)
Per semplicita', si supponga di aver gia' dimostrato che le stringhe riconosciute dall'automa siano tutte della forma aⁿb. Si dimostri quindi solamente che tutte quelle della forma aⁿb sono riconosciute.