Un'algebra e' un insieme I a cui sono associate alcune operazioni.
Un'algebra si dice booleana (o di Boole) se:

l'insieme I contiene due elementi distinti (che per convenzione possiamo indicare con "0" e "1")
abbiamo tre operazioni sull'insieme, due binarie ed una unaria (che per convenzione possiamo indicare con "+", "." "^-". L'operatore "." tradizionalmente si indica con la semplice giustapposizione degli operandi)
i seguenti assiomi risultano soddisfatti:
P₁) x + 0 = x
P₂) x + 1 = 1
P₃) x + x = x
P₄) x + x^- = 1
P₅) x₁ + x₂ = x₂ + x₁ (commutativita' della somma)
P₆) (x₁ + x₂) + x₃ = x₁ + (x₂ + x₃) (associativita' della somma)
P₇) (x₁x₂) + (x₁x₃) = x₁(x₂ + x₃) (distributivita' della prodotto rispetto alla somma)

P'₁) x1 = x
P'₂) x0 = 0
P'₃) xx = x
P'₄) xx^- = 0
P'₅) x₁x₂ = x₂x₁ (commutativita' del prodotto)
P'₆) (x₁x₂)x₃ = x₁(x₂x₃) (associativita' del prodotto)
P'₇) (x₁ + x₂)(x₁ + x₃) = x₁ + (x₂x₃) (distributivita' della somma rispetto al prodotto)

P₈) (x^-)^- = x (involuzione della negazione)

Gli assiomi P₁-P₇ e P'₁-P'₇ sono gli uni duali degli altri (si ottengono gli uni dagli altri sostituendo la somma con il prodotto, lo "0" con "1" e viceversa.) Questo fatto e' alla base del principio di dualita' delle algebre booleane: una proprieta' e' valida se e solo se e' valida anche la sua duale.
Per convenzione, per risparmiare di scrivere parentesi) l'operatore prodotto ha precedenza sulla somma ed a sua volta e' preceduto dalla negazione. Esempio: xy^- + z significa ((x(y^-)) + z)
Notare come dagli assiomi dati derivi il comportamento funzionale di "+", "." e "^-", che si puo' esprimere con delle tavole di verita' o con le seguenti affermazioni
(x + y) = 0 SSE x = y = 0
xy = 1 SSE x = y = 1
x^- = 0 SSE x = 1

Esempi di algebre booleane

Prendiamo un insieme A qualsiasi e prendiamo come I l'insieme delle parti di A (tutti i sottoinsiemi di A). Come "0" prendiamo l'insieme vuoto e come "1" l'intero insieme A. Come somma consideriamo l'operatore di unione insiemistica, come prodotto l'intersezione insiemistica e come negazione l'operatore di complemento insiemistico rispetto ad A.
Si puo' vedere come esercizio che quella che abbiamo descritta e' un'algebra booleana, poiche' tutti gli assiomi risultano verificati.
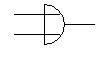
Prendiamo un'altra struttura in cui I sia un insieme di due soli elementi, per esempio due differenti livelli di tensione: { 0Volt, +5Volt}. Come operatore di somma prendiamo una componente elettronica (porta OR) con due segnali di ingresso (t₁ e t₂) ed uno di uscita (t₃) tale che t₃ = 0Volt SSE t₁ = t₂ = 0Volt e lo indichiamo graficamente con

Come operatore prodotto prendiamo una componente elettronica (porta AND) con due segnali di ingresso (t₁ e t₂) ed uno di uscita (t₃) tale che
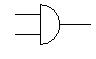
t₃ = +5Volt SSE t₁ = t₂ = +5Volt e lo indichiamo graficamente con

mentre come negazione la componente elettronica (NOT) con un segnale di ingresso (t₁) ed uno di uscita (t₂) tale che
t₃ = +5Volt SSE t₁ = 0Volt e lo indichiamo graficamente con

Si puo' facilmente vedere per esercizio che questa che abbiamo descritto e' anch'essa un'algebra di Boole, poiche' gli assiomi sono tutti verificati dalla nostra struttura.

Per essere precisi, i valori di tensione reali e le componenti elettroniche reali illustrate nell'esempio precedenti sono da considerarsi come rappresentazioni fisiche di una particolare struttura matematica chiamata Algebra Booleana Minimale o anche Algebra Binaria di Commutazione (Switching Algebra in inglese).
E' immediato notare come nella Switching Algebra si possa interpretare lo "0" come il valore di verita' FALSO, l'"1" come VERO e gli operatori come i connettivi logici AND, OR e NOT.

Ogni funzione n-aria su {0,1} e' esprimibile come espressione algebrica. Questo fatto e' dimostrato dall'esistenza delle forme canoniche (vedi Luccio-Pagli). Questo significa che, data una funzione booleana, possiamo sempre costruire un circuito che la calcola.

Se a partire dagli assiomi dell'Algebra Booleana riusciamo a dimostrare alcune proprieta' (per esempio che x₁x₂ + x₁x^-₂ = x₁), allora queste proprieta' saranno vere in tutte le possibili algebre booleane. In particolare nella Switching Algebra. Possiamo quindi dimostrare proprieta' di circuiti logici dimostrando proprieta' dell'algebra booleana.

Se siamo interessati in proprieta' di tutte le algebre booleane che siano proprieta' esprimibili sotto forma equazionale (del tipo x₁x₂ + x₁x^-₂ = x₁) oppure se siamo interessati esclusivamente in proprieta' della Switching Algebra (e quindi dei circuiti) allora abbiamo un'altra metodologia di dimostrazione: basta vedere se la proprieta' e' soddisfatta da ogni possibile assegnazione di valori 0, 1 alle variabili.
Questo significa che se vogliamo dimostrare la validita' di una delle leggi di De Morgan per due variabili: (x + y)^- = x^-y^- possiamo dimostrarla vedendo che
(0 + 0)^- = 0^-0^-
(0 + 1)^- = 0^-1^-
(1 + 0)^- = 1^-0^-
(1 + 1)^- = 1^-1^-

Utilizzando il principio' di dualita' possiamo dedurre da (x + y)^- = x^-y^- anche l'altra legge di De Morgan per due variabili, e cioe' (xy)^- = x^- + y^-

Il seguente "Teorema del Consenso": xy + x^-z + yz = xy + x^-z. e' dimostrabile, cosi' come abbiamo fatto con De Morgan, provando tutti i possibili assegnamenti di valori alle tre variabili, oppure utilizzando gli assiomi. Infatti
xy + x^-z + yz = (per P'₁ e P₄)
xy + x^-z + (x + x^-)yz = (per commutativita' e distributivita')
(xy + xyz) + (x^-z + x^-yz) = (per P'₁, commutativita' e distributivita')
xy(1 + z) + x^-z(1 + y) = (per P₂ e P'₁)
xy + x^-z

Il teorema del consenso significa, per esempio, che siamo sicuri che il due circuiti seguenti sono equivalenti (calcolano cioe' la stessa funzione booleana). Avendo uno meno porte logiche dell'altro questa proprieta' ci permette di semplificare circuiti.