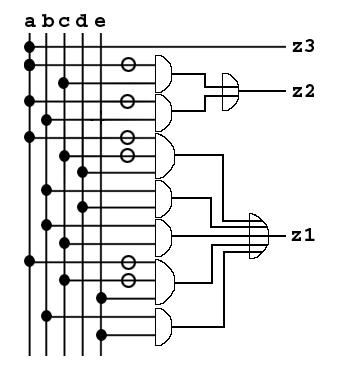
Ideare un circuito a cinque ingressi che restituisca in output la codifica binaria della radice quadrata arrotondata per difetto del numero binario inserito come input.

Come prima considerazione bisogna notare che un numero binario a 5 bit (a,b,c,d,e) è compreso tra 0 e 31 (in decimale) e quindi per rappresentare la radice quadrata abbiamo bisogno dei 3 bit (z1,z2,z3), che permettono di codificare numeri compresi tra 0 e 7, anche se noi non necessitiamo dei numeri 6 e 7, perchè la radice quadrata arrotondata per difetto di 31 è 5 (101 in binario).
Quindi possiamo dividere i nostri input in 5 gruppi, a seconda della loro radice e schematizzare l'utilizzo dei 3 bit di output così come segue:

Il bit z1 ha valore 1 per input (decimali):
{1,2,3,9,10,11,12,13,14,15,25,26,27,28,29,30,31}

Il bit z2 ha valore 1per input (decimali):
{4,5,6,7,8,9,10,11,12,13,14,15}

Il bit z3 ha valore 1 per input (decimali):
{16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31}

Ciò che bisogna fare adesso è creare 3 mappe di Karnaugh a 5 variabili, una per ciascuno dei bit di output, e ricavare da ciascuna di esse la forma SP minimale.
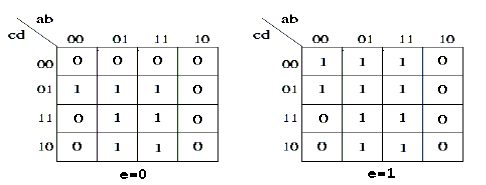
Iniziamo considerando il bit z1, la sua mappa di Karnaugh è:

Tracciamo gli implicanti essenziali in rosso, o in blu nel caso che l'implicante comprenda sia elementi della mappa per e=0, sia per quella e=1, per poi scrivere la forma SP minimale (indico con a' la negazione di a):

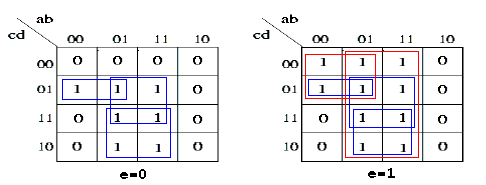
f(a,b,c,d,e) = a'c'd + bd + bc +a'c'e + be

Analogamente procediamo per il bit z2:

e tracciamo gli implicanti essenziali, ottenendo:

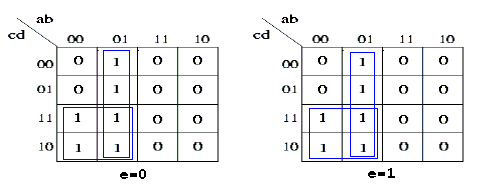
f(a,b,c,d,e) = a'c + a'b

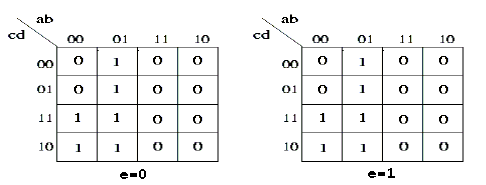
Infine rappresentiamo la mappa di Karnaugh per il bit z3:

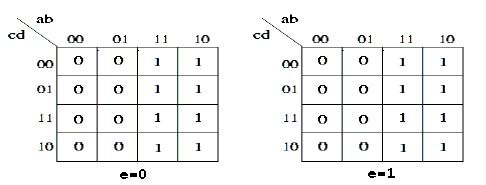
anche in questo caso ricaviamo la forma SP minimale:

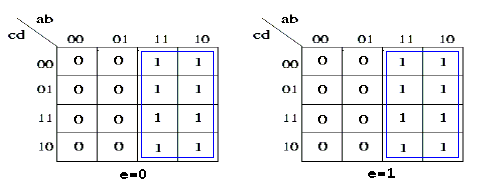
f(a,b,c,d,e) = a

Unificando queste tre reti in un unico blocco combinatorio a cinque ingressi (a,b,c,d,e) e tre uscite (z1,z2,z3) si ottiene: