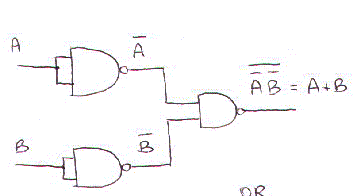
-   Disegnare lo schema logico che realizza la funzione OR
  utilizzando solo porte logiche NAND. Mostrare i passi logici
  (utilizzando le proprieta` dell'algebra di Boole) che dimostrano la
  correttezza di tale schema.


SOLUZIONE:

	Una porta NAND produce come out not(AB). Basterà negare il risultato utilizzando una 
	porta NAND con gli ingressi uniti ottenendo:

		not(not(AB)) = AB

==========================================================================================
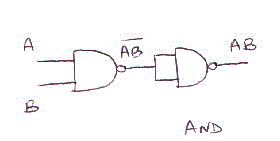
-   Disegnare lo schema logico che realizza la funzione AND
  utilizzando solo porte logiche NAND.



SOLUZIONE:

	A + B => (per la pr. involutiva) = not(not(A + B) => (Applicando De Morgan) =

	= not(not(A) not(B))

	In base a questa relazione il circuito si puo' realizzare come in figura:

==========================================================================================
- Sia F una funzione di 4 variabili definita da 
  F= not{A} not{B} C not{D} +
     A not{B} not{C} not{D} + 
     A not{B} C D + 
     A not{B} C not{D} 
  e tale per cui sappiamo che le configurazioni di input
  not{A} not{B} not{C} not{D} e A not{B} not{C} D 
  non si presentano mai. Minimizzare
  l'espressione di F tramite mappa di Karnaugh. (Suggerimento:
  utilizzare valori ``don't care'' per le configurazioni di input
  indicate.)



SOLUZIONE:

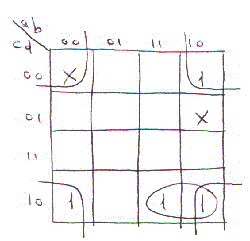
	La mappa di Karnough e' quella della figura Da essa si ottiene:

		F = not(B) not(D) + A C not(D)