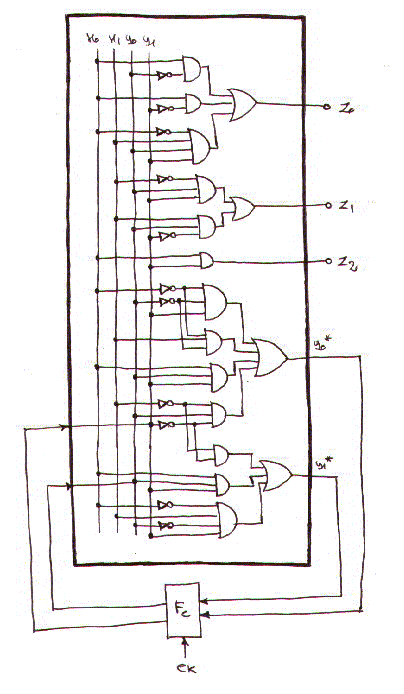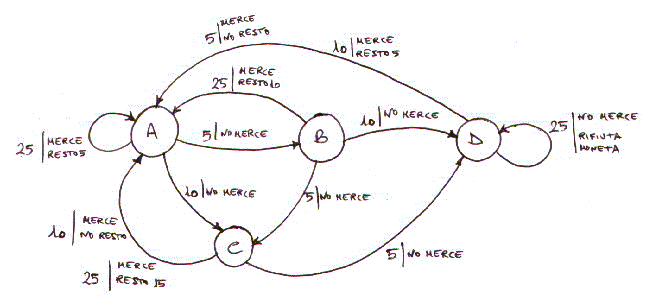
Progettare un controller per un distributore automatico che accetta tre tipi di monete di 
valore 5,10 e 25, rispettivamente. La merce viene erogata al raggiungimento del valore 20. 
Il distributore prevede un resto massimo di una moneta da 5 e di una da 10. 
==========================================================================================
SOLUZIONE:

Descriviamo l'automa a stati finiti. Gli ingressi sono:

            X = {moneta da 5, moneta da 10, moneta da 25}

le uscite sono:

            Z = {Nessuna merce, Nessuna merce rifiuta la moneta, Merce senza resto,
                 Merce con resto 5, merce con resto 10, merce con resto 15} 

  
Per gli stati invece abbiamo:

            S = {A,B,C,D}    

dove:

       A = Nessun credito

       B = Credito 5

       C = Credito 10

       D = Credito 15

Il diagramma di flusso sara' il seguente:

Da esso otteniamo la seguente tabella delle transizioni:

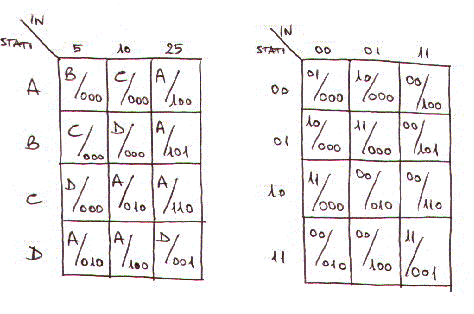
Abbiamo effettuato le seguenti codifiche:

   STATI     INPUT                     OUT
  -------   ------------------        ------------------------------
   A=00      Moneta da  5 = 00         No merce = 000
   B=01      Moneta da 10 = 01         No merce, rifiuta moneta = 001
   C=10      Moneta da 15 = 11         Merce, nessun resto = 010
   D=11                                Merce, resto 5 = 100
                                       Merce, resto 10 = 101
                                       Merce, resto 15 = 110


Con questa codifica il bit piu' significativo dell'OUT vale 1 se e solo se si ha un resto.
Come si osserva da essa non esistono stati che a parita' di input hanno la stessa uscita quindi
non vale la prima proprieta' che deve valere per minimizzare un automa per cui l'automa risulta
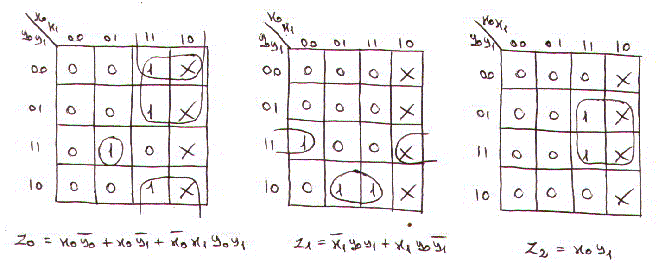
minimo. Per la parte combinatoria otteniamo le seguenti mappe di karnaugh:

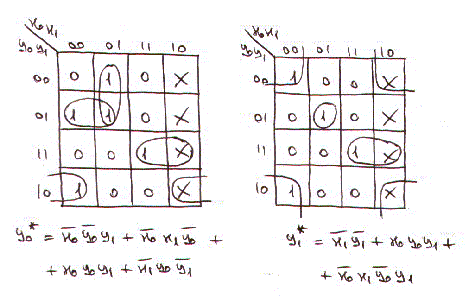
Il controller progettato sara' il seguente: