Progettare una macchina a stati finiti che manda in output 1 quando esattamente due
degli ultimi 3 input sono a 1. Si assume come input una linea seriale ad 1 bit.

====================================================================================

Descriviamo l'automa a stati finiti. Gli input sono:

           X = {0, 1}

le uscite sono:

           Z = {0, 1}

e gli stati interni sono:

           S = {A, B, C, D, E}


dove:

           A = stato iniziale

           B = E' arrivato 0

           C = E' arrivato 1

           D = l'input precedente e' la sequenza 0 1
 
           E = l'input precedente e' la sequenza 1 0


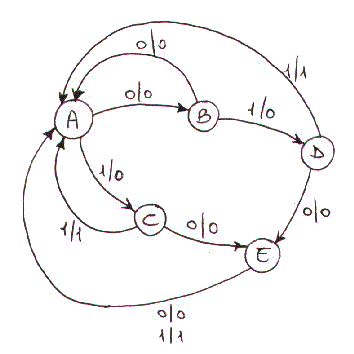
Il diagramma di flusso sara' il seguente:

da cui otteniamo la seguente tabella delle transizioni:

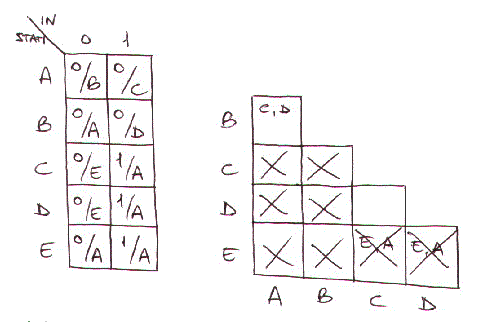
Proviamo a semplificare l'automa a stati finiti. Alla fine del processo di semplificazione 
(come si vede dalla figura precedente) si ottengono le seguenti classi di equivalenza:

             [A,B], [C,D], [E]

che chiamiamo rispettivamente alfa, beta e gamma. Otterremo allora il nuovo automa a
stati finiti avente gli stessi X e Z del precedente, ma avente gli stati:

            S = {alfa, beta, gamma}

e la seguente tabella delle transizioni:

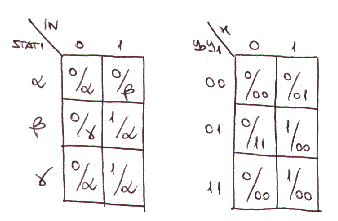
in cui abbiamo codificato:
            alfa = 00
            beta = 01
           gamma = 11

Costruiamo infine il circuito sequenziale. Le mappe di karnough relative alla parte
combinatoria sono:

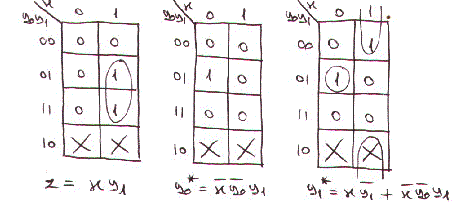
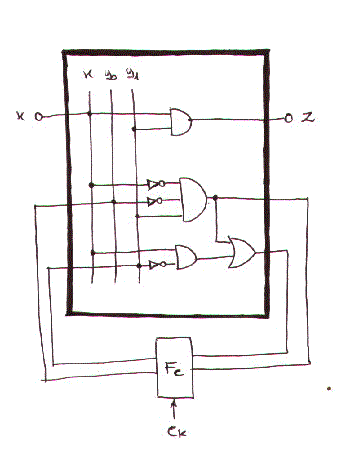
Otteniamo quindi il seguente circuito: