Abbiamo una rete combinatoria con 4 ingressi (x3, x2, x1, x0) e sette uscite (z6, z5, z4, z3, z2, z1, z0) che accendono rispettivamente la lampadina n. 6, n. 5, e cosė via.
	Servendomi  delle MAPPE DI KARNAUGH ricavo le uscite relative alle funzioni:
Z'6, Z'5, Z'4, Z'3, Z'2, Z'1, Z'0.
La lampadina Zi   (con 0<= i=<6) si accende quando la rete prende in ingresso i seguenti numeri:

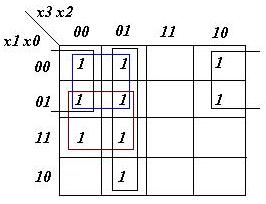
-  Z'6= (0, 2, 3, 5, 6, 8)   

       z6= x1x3'x2' + x1x0'x3' + x1'x0x3'x2 + x1'x0'x2'


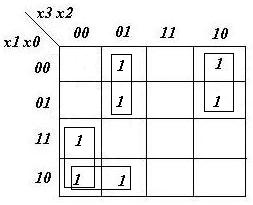
- Z'5= (0, 1, 3, 4, 5, 6, 7, 8, 9)  

       z5= x3'x2 + x0x3' + x1'x2'


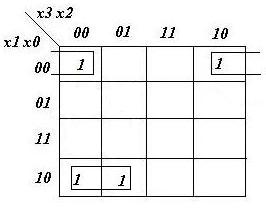
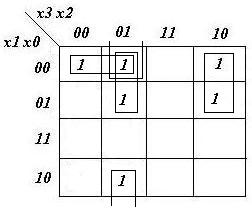
- Z'4= (0, 2, 6, 8) 
 
      z4= x3'x1x0' + x1'x0'x2'

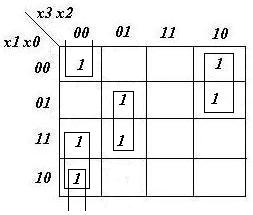
- Z'3= (2, 3, 4, 5, 6, 8, 9) 
 
      z3= x1x3'x2' + x1x0'x2 + x1'x3'x2 + x1'x3x2'



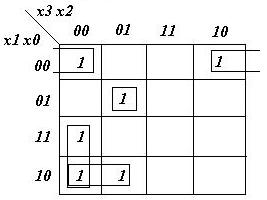
- Z'2= (0, 1, 2, 3, 4, 7, 8, 9)        

      z2= x3'x2' + x2'x1' + x1'x0'x3' + x1x0x3'



-  Z'1= (0, 4, 5, 6, 8, 9)       

      z1= x1'x0'x3' + x1'x3'x2 + x1'x3x2' + x0'x3'x2


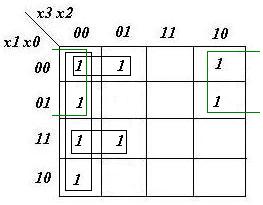
-  Z'0= (0, 2, 3, 5, 7, 8, 9)    

      z0= x1x3'x2' + x0'x3'x2' + x0x3'x2 + x1'x3x2'


Quindi, la rete combinatoria e' cosi' costituita: