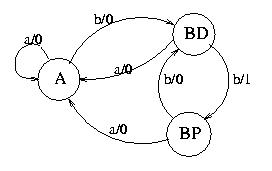
Possiamo ora costruire la tabella di flusso (che poi non e' altro che una diversa rappresentazione del diagramma):

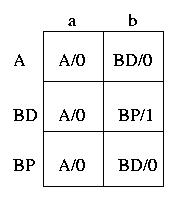
Ora codifichiamo con stringhe binarie gli stati di ingresso e gli stati interni (la codifica di quelli di uscita e' ovvia). (Da ricordare, anche se non lo facciamo, come in realta' tali codifiche andrebbero fatte scegliendo quelle codifiche che permettano di arrivare a circuiti combinetori i piu' semplici possibili).

a = 0
b = 1

A = 00
BD = 01
BP = 10

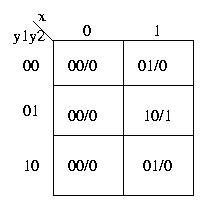
A questo punto , indicando con x i segnali che codificano gli stati di ingresso, con y1 e y2 quelli che codificano gli stati interni e con z il segnale che codifica la configurazione di uscita, otteniamo, a partire dalla tabella di flusso, la tabella delle transizioni.

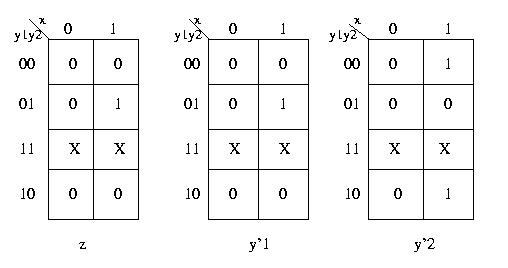
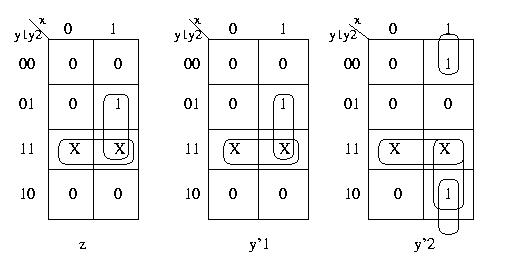
Dalla tabella delle transizioni possiamo facilmente ottenere le mappe di Carnaugh per le 3 funzioni booleane z, y'1 e y'2 (y'1 e y'2 rappresentano lo stato interno "successivo"). Notare come, avendo due bit per la codifica dello stato interno e solo tre stati interni, alcune caselle delle mappe di Carnaugh risultino indeterminate.

Adesso possiamo sintetizzare i circuiti combinatori per z, y'1 e y'2, notando che le funzioni z e y'1 sono identiche. Visto che e' indifferente considerare le X come 0 o come 1, le consideriamo come 1, poiche', visto che vogliamo ottenere forme SP minimali, questo permette di ottenere implicanti primi "piu' grandi".
E' importante notare come la particolare codifica che abbiamo dato degli stati interni ci ha permesso di

A questo punto, le espressioni SP minimali sono le seguenti, tenendo conto che per ottenerle non bisogna prendere in considerazione implicanti primi che coprano solo valori indeterminati o che sono rilevanti solo per valori indeterminati (per esempio, l'implicante y1x ha il suo vero 1 coperto da un implicante essenziale, not(y2)x, e quindi possiamo non considerarlo, visto che l'altro valore che copre e' indeterminato).

z = y'1 = y2x

y'2 = not(y2)x

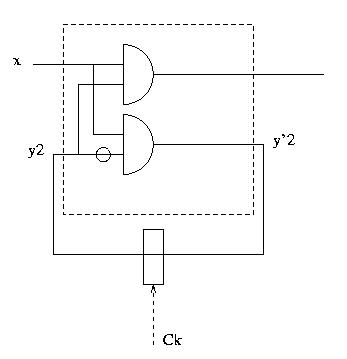
E' interessante notare come y1 non compaia tra i segnali della rete sequenziale. Questo si spiega con il fatto che il nostro automa a stati finiti che abbiamo sviluppato all'inizio possiede degli stati ridondanti. La presenza di stati ridondanti in un automa a stati finiti si puo' determinare con un semplice algoritmo, che pero' non abbiamo studiato a lezione e la cui applicazione ci avrebbe permesso di partire da un automa piu' semplice e quindi arrivare piu' semplicemente al al nostro risultato che, in questo caso particolare, fortuitamente, e' lo stesso che si sarebbe ottenuto utilizzando l'algoritmo di minimizzazione di automi.
Notare come, utilizzando il nostro automa, ma codificando diversamente gli stati interni, potevamo arrivare ad una soluzione piu' complessa.
Se infatti codificavamo BP con 11, avremmo avuto, per z, la seguente mappa di Carnaugh,

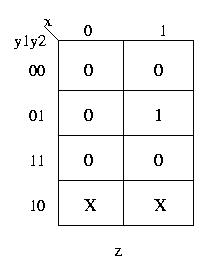
ottenendo cosi' come espressione per z la seguente:

z = not(y1)y2x

Da una analisi piu' attenta, senza dover ricorrere all'algoritmo di minimizzazione degli automi, si puo' vedere come il seguente automa sia piu' piccolo ed equivalente a quello che abbiamo fornito.

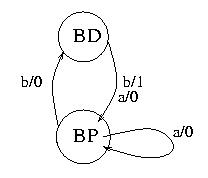
Infatti lo stato BP si puo' intendere come:
ho appena ricevuto una a oppure ho appena ricevuto un numero pari di b consecutive.
Lo stato BP e' anche quello iniziale.

L'ideale sarebbe stato quindi partire con tale automa, grazie all'algoritmo di minimizzazione o grazie ad un'analisi piu' acuta.
Il processo di sintesi sarebbe stato, piu' semplicemente, il seguente.

Tabella di flusso:

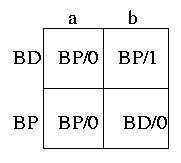
Codifica:
BP = 0
BD = 1
a = 0
b = 1

Tabella delle transizioni:

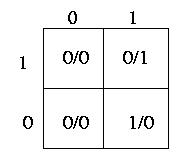
Dalla tabella delle transizioni possiamo facilmente ottenere le mappe di Carnaugh per le 2 funzioni booleane z e y' (y rappresenta lo stato interno "successivo").

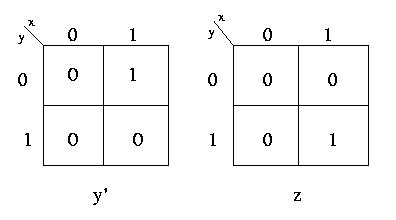
Per ogni mappa abbiamo un unico implicante primo, che e' anche un mintermine.

y' = xnot(y)

z = xy

Notare come, in questo caso particolare, arriviamo allo stesso circuito a cui eravamo arrivati partendo dall'automa non minimizzato.