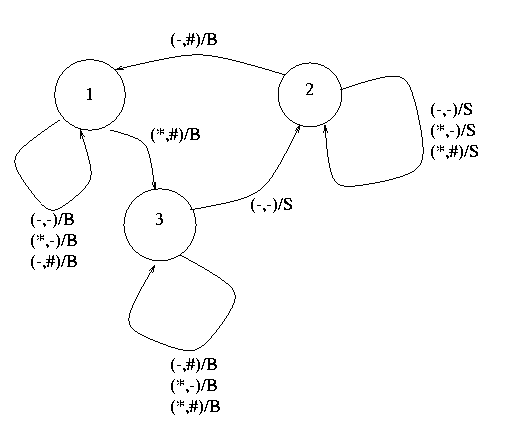
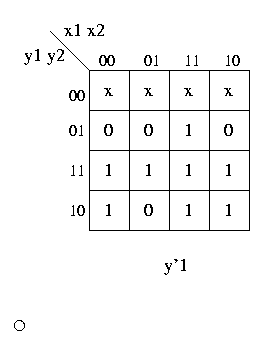Per risolvere il problema possiamo introdurre un nuovo stato: 3,
che permette di non "sentire" le configurazioni intermedie durante
la transizione da (*,#) a (-,-). Il diagramma risultante e' il seguente:
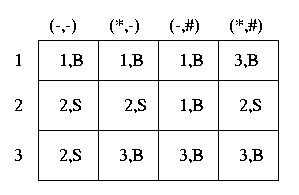
Possiamo ora costruire la tabella di flusso (che poi non e' altro che una diversa
rappresentazione del diagramma):
Ora codifichiamo con stringhe binarie le configurazioni di ingresso, gli stati interni
e le conficurazioni di uscita:
(-,-) = 00
(*,-) = 10
(-,#) = 01
(*,#) = 11
1 = 01
2 = 10
3 = 11
B = 1
S = 0
A questo punto , indicando con x1 e x2 i segnali che codificano le configurazioni di
ingresso, con y1 e y2 quelli che codificano gli stati interni e con z il segnale
che codifica la configurazione di uscita, otteniamo, a partire
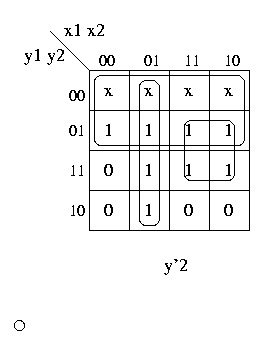
dalla tabella di flusso, le 3 mappe di carnaugh per le 3 funzioni booleane z, y'1 e y'2
(y'1 e y'2 rappresentano lo stato interno "successivo").
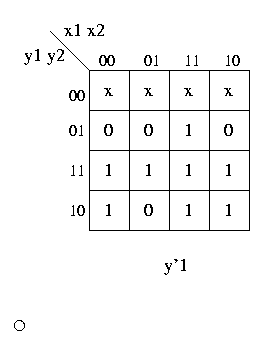
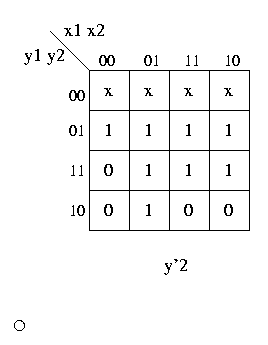
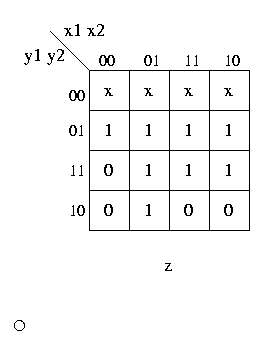
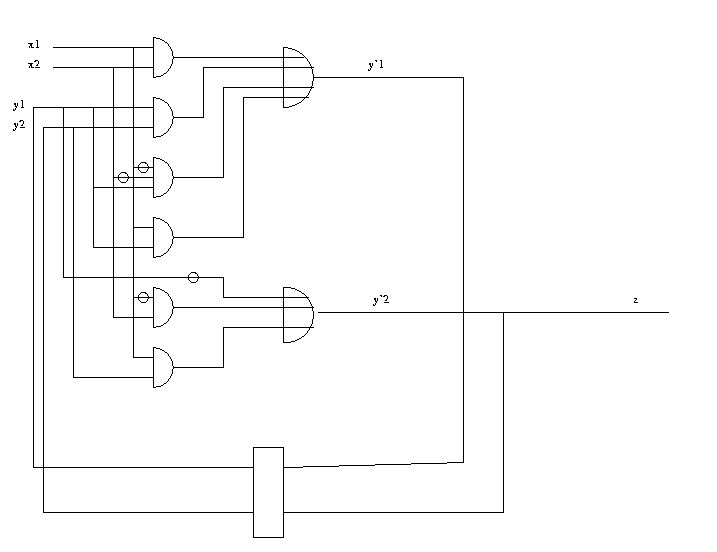
Adesso possiamo sintetizzare i circuiti combinatori per z, y'1 e y'2, notando che
le funzioni z e y'2 sono identiche.
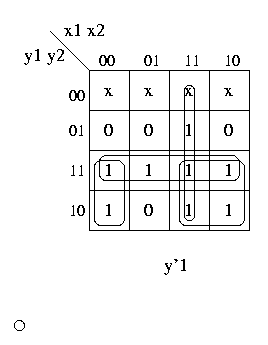
y'1 = x1x2 + y1y2 + notx1notx2y1 + x1y1
y'2 = noty1 + notx1x2 + x1y2
z = y'2
La rete sequenziale sara' quindi