Gli Ingressi del nostro automa saranno
X = {0,1}
le uscite
Z = {0,1}
Per gli elementi di X e Z non c'e' bisogno di codifica (si potrebbe codificare
0 con 1 ed 1 con 0 se questo portasse a mappe di Karnaugh piu' semplici, ma
non ci poniamo questo problema).
Il nostro automa avra' bisogno di 5 stati interni per poter ricordarsi
quale parte dell'eventuale sequenza "1100" e' gia' arrivato, piu' lo
stato iniziale. Vedremo poi con la minimizzazione se sara' possibile
avere meno stati.
Quindi
S = {A,B,C,D,E}
Il diagramma degli stati e la relativa tabella di flusso sono:
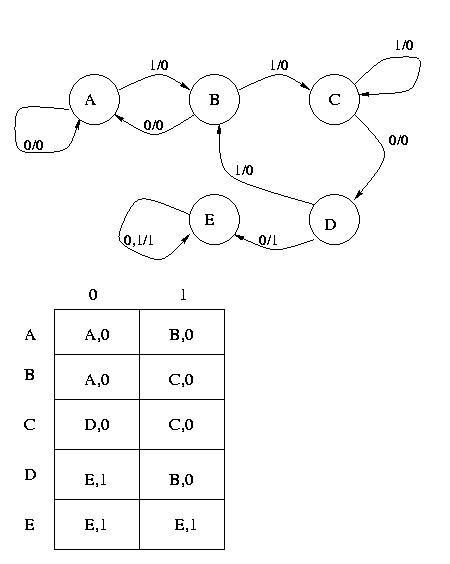
Applichiamo il metodo di minimizzazione, construendo
la tabella a scala e vediamo che il
procedimento di minimizzazione termina con 4 iterazioni
e produce, dopo la quarta iterazione, la seguente tabella.
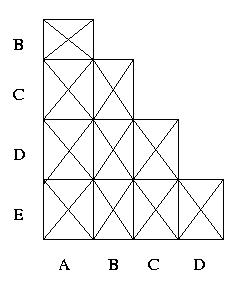
L'insieme degli stati si puo' quindi partizionare in classi di stati equivalenti
che sono dei singoletti:
(A), (B), (C), (D) (E)
Il nostro automa era quindi minimo.
Codifichiamo ora gli elementi di S.
A : 000
B : 001
C : 010
D : 011
E : 100
Ovviamente la codifica la facciamo a caso, senza preoccuparci di eventuali
ottimizzazioni che potrebbero esserci se codificassimo differentemente.
Dalla tabella di flusso otteniamo, con le date codifiche, la seguente tabella
delle transizioni.
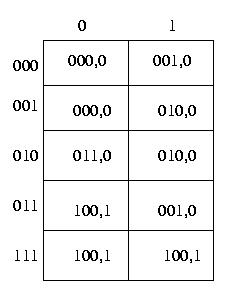
Da questa si ottengono le mappe di Karnaugh per l'unica uscita e i tre
segnali che codificano lo stato interno successivo.
In questa soluzione non vengono indicate queste mappe di Karnaugh, ne' le
rispettive espressioni algebriche minimali, ne' il circuito sequenziale
che ne vien fuori, visto che dovreste saperlo fare bene, considerando tutti
gli esercizi che gia' son disponibili.


