Descriviamo prima l'automa a stati finiti che descrive il comportamento che dovra' avere in nostro circuito.
L'insieme degli Input sara': X = {0,1}
Quello degli Output: Z = {0,1,2,3,4}
Gli stati interni dovranno rappresentare l'informazione riguardo i bit che sono gia' stati forniti in ingresso, quindi, usando dei nomi un minimo sognificativi avremo: S = { I, 0, 1, 00, 01, 10, 11}
Il diagramma degli stati sara':

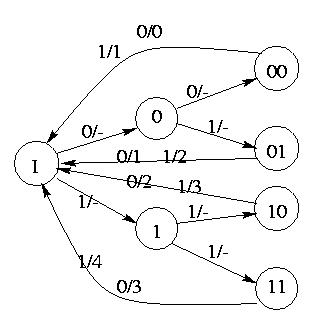
Notare che non abbiamo specificato l'output laddove e' ininfluente. La mancata specificazione portera' a mappe di Karnaugh non completamente specificate.

Passiamo ora alla tabella di flusso

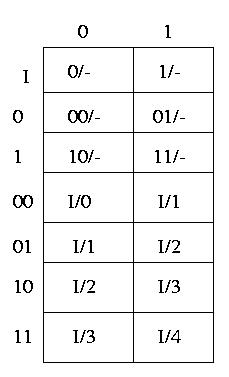
Codifichiamo gli elementi di X, Z e S per passare cosi' alla tabella delle transizioni ed alle mappe di Karnaugh. Nella codifica non terremo conto del fatto che alcune codifiche potrebbero portare ad ottenere alla fine crcuiti piu' semplici.

X, ovvio. Per Z, la soluzione piu' ragionevole e' fornire in output al circuito la rappresentazione binaria dei valori.
Quindi:
0 --> 000
1 --> 001
2 --> 010
3 --> 011
4 --> 100

Per S, visto che non abbiamo il voncolo di cercare la codifica ottimale, forniamo una codifica che ci aiuti a non fare (troppi) errori al momento di scrivere le mappe di Karnaugh a partire dalla tabella delle transizioni. Poiche' abbiamo 7 elementi in S, avremo bisogno di 3 bit per codificarli:
I --> 111
0 --> 000
1 --> 100
00 --> 001
01 --> 011
10 --> 101
11 --> 111

A questo punto non e' difficile descrivere le mappe di Karnaugh e sintetizzare la rete.