x1 x2 x3 | u
0   0   0  | 0
0   0   1  | 1
0   1   0  | 1
0   1   1  | 0
1   0   0  | 1
1   0   1  | 0
1   1   0  | 0
1   1   1  | 1

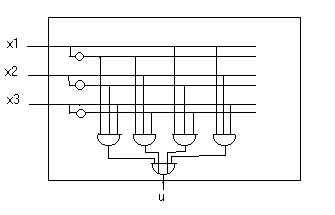
u =  x1'x2'x3 + x1'x2x3' + x1x2'x3' + x1x2x3
quindi il circuito è :

A questo punto, per realizzare la codifica, si deve sfruttare il circuito precedente ( che chiamo PARITY ) come è mostrato nella seguente figura:

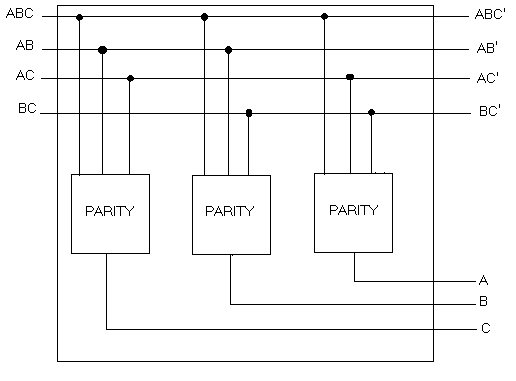
Gli ingressi del circuito sono ABC, AB, AC, BC.
Osservando la seguente figura si capisce che gli ingressi rappresentano i bit contenuti nella parte evidenziata dalla freccia:

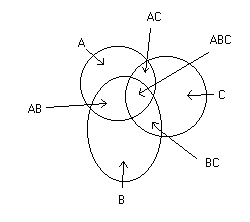
Le uscite ABC',AB',AC' e BC' hanno gli stessi valori dei relativi ingressi. ( il simbolo ' non significa "negato" ma "primo")
Mentre le uscite A,B e C  sono i bit di parità e sono anch'essi evidenziati dallo schema sovrastante.
Vengono così aggiunti 3 bit di ridondanza ai 4 bit che rappresentano il numero tra 0 e 15 in binario.

Riguardo la decodifica bisogna riutilizzare il blocco realizzato per la codifica (che chiamo HAMMING) poichè va calcolata anche qui la parità dei bit che rappresentano l'informazione. In seguito, vanno confrontati i 3 bit ridondanti calcolati nella codifica con quelli della decodifica. Il confronto dei bit, tramite la porta XOR ( che restituisce 0 se a=b ), permetterà di pilotare dei selettori che avranno lo scopo di modificare il bit errato.
Più precisamente:
il selettore relativo a BC inverte l'ingresso BC' se (B\=B' e C\=C')
il selettore relativo a AC inverte l'ingresso AC' se (A\=A' e C\=C')
il selettore relativo a AB inverte l'ingresso AB' se (A\=A' e B\=B')
il selettore relativo a ABC inverte l'ingresso ABC' se (A\=A' e B\=B' e C\=C')
essendo A',B' e C' i bit ridondanti calcolati nella codifica e A,B e C quelli calcolati nella decodifica.
Si ottiene così il seguente circuito:

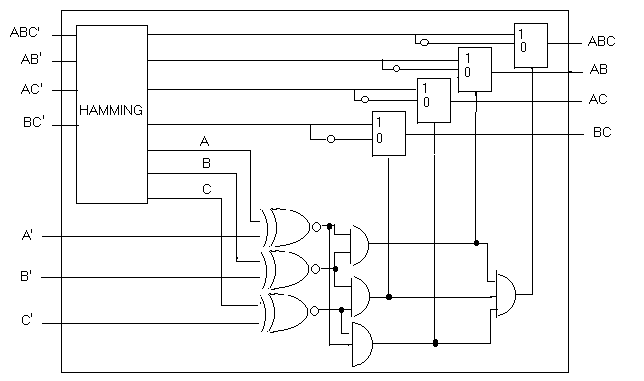
In definitiva, in questo circuito gli ingressi ABC',AB',AC',BC',A',B',C' è l'informazione espressa con il codice di Hamming e le uscite ABC,AB,AC,BC sono i bit che rappresentano l'informazione originaria.Se si è verificato un errore, questo viene corretto.