Iniziamo con la descrizione dell'automa a stati finiti.
L'insieme dei suoi ingressi sara':

X = { Ness, In1, In2, In3}

Ness indica che non c'e' alcun visitatore
Inj indica che il visitatore e' nella sezione j.

Z = { 0, 1 }

0 e' il segnale che tiene spenta la registrazione.
1 e' il segnale che tiene accesa la registrazione.

S = { A, B, C, D }

A e' lo stato che indica che nessuno ha iniziato il giro o che il visitatore ha fatto una cosa in violazione di quanto scritto;
B e' lo stato che indica che il visitatore e' nella Sezione 1 senza contravvenire alle disposizioni del cartello;
C e' lo stato che indica che il visitatore e' nella Sezione 2 senza contravvenire alle disposizioni del cartello;
D e' lo stato che indica che il visitatore e' nella Sezione 3 senza contravvenire alle disposizioni del cartello;

Per descrivere l'automa notiamo come le disposizioni del cartello non impediscano a chi ha appena visitato la sezione 2, di rivisitare la 1 e la 2 prima di passare alla 3, oppure di rivisitare la 2 o la 1 e la 2 dopo aver visitato la 3.

Il diagramma degli stati e la relativa tabella di flusso sono:

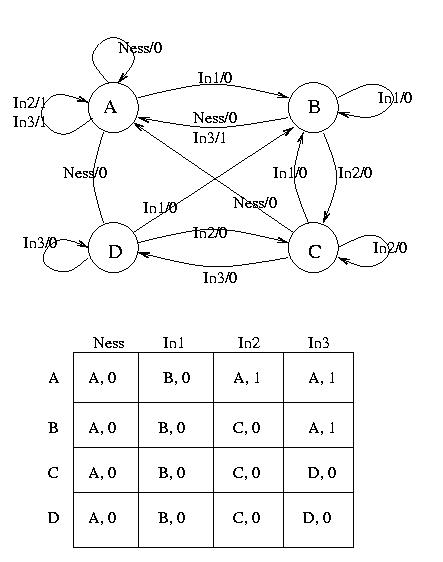
E immediato vedere che l'automa descritto non e' minimo, poiche' gli stati C e D sono banalmente equivalenti. Comunque, visto che il testo lo richiede, applichiamo il metodo di minimizzazione, construendo la tabella a scala.
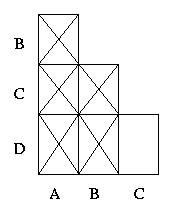Il procedimento di minimizzazione termina con 0 iterazioni.
L'insieme degli stati si puo' quindi partizionare in classi di stati equivalenti:
(A), (B), (C, D)

Indichiamo con CD lo stato ottenuto dalla fusione degli stati equivalenti C e D, ottenendo l'automa minimale descritto dalla seguente tabella di flusso.

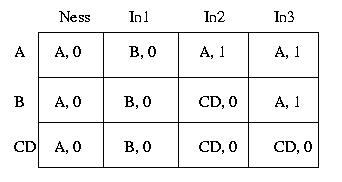
Codifichiamo ora gli elementi di X e S (quelli di Z li codifichiamo con il loro nome).
Ness: 00
In1 : 01
In2 : 11
In3 : 10

A : 00
B : 01
CD: 11

Dalla tabella di flusso otteniamo, con le date codifiche, la seguente tabella delle transizioni.

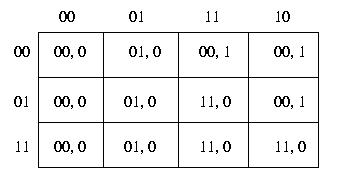
Da questa otteniamo le mappe di Karnaugh per l'unica uscita e i due segnali che codificano lo stato interno successivo.
Notare come le tre funzioni possano essere coperte dai soli implicanti primi essenziali.


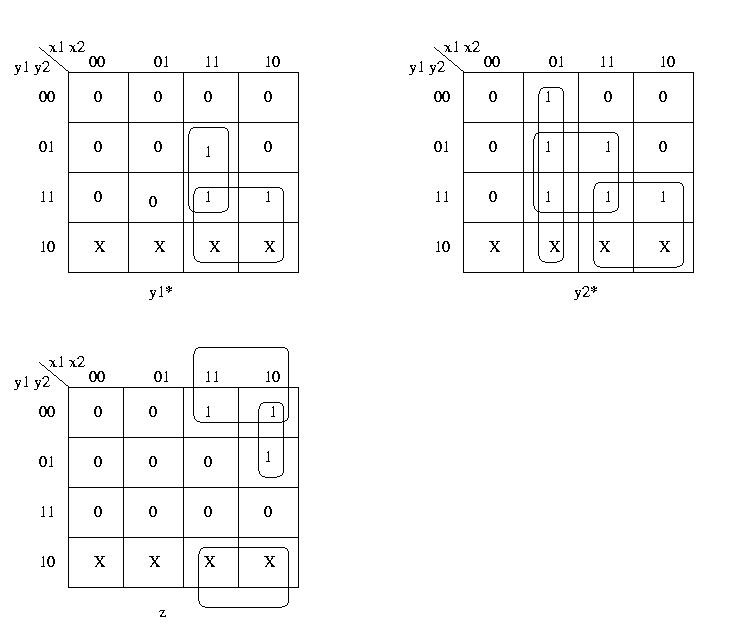
Le tre funzioni sono quindi descritte dalle seguenti espressioni algebriche minimali.

y1* = x1y1 + x1x2y2

y2* = x1y1 + x2y2 + (notx1)x2

z = x1(noty2) + x1(notx2)(noty1)

Da cui otteniamo la seguente rete sequenziale sincrona:


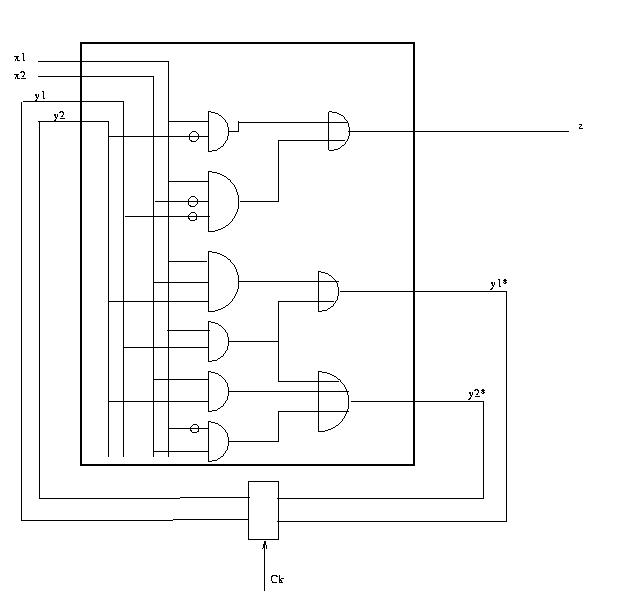
Notare come nelle funzioni y1* e y2* abbiamo messo in comune l'implicante x1y1.

Nella sintesi non abbiamo visto se una differente codifica degli elementi di X, Z e S avrebbe potuto portare ad una rete piu' semplice.

---