Descriviamo l'automa a stati finiti. Gli ingressi sono:

                X = {0,1}

le uscite:
       
                Z = {0,1}

gli stati interni:

                S = {A,B,C,D,E,F,G}

dove:

        A = {t = 4k}  

        B = {t = 4k+1 e l'input all'istante t=4k e' x=0}

        C = {t = 4k+2 e l'input all'istante t=4k e' x=0}

        D = {t = 4k+3 e l'input all'istante t=4k e' x=0} 

        E = {t = 4k+1 e l'input all'istante t=4k e' x=1}

        F = {t = 4k+2 e l'input all'istante t=4k e' x=1}

        G = {t = 4k+3 e l'input all'istante t=4k e' x=1}


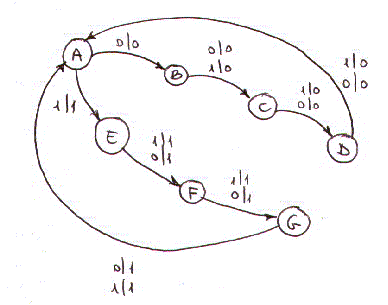
Il tutto per per k = 0,1,2,.... Il diagramma di flusso e' il seguente:

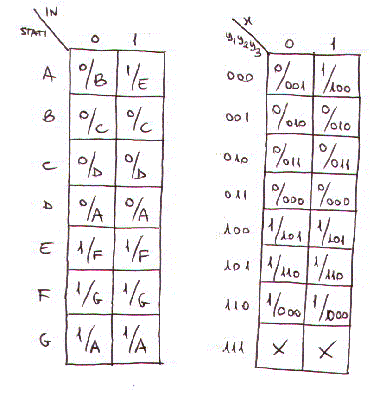
Da cui si ottengono le seguenti tabelle degli stati:

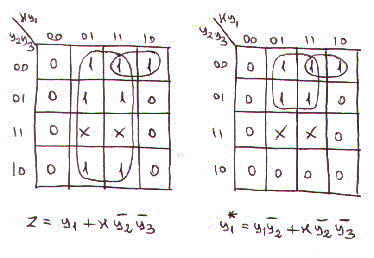
Le mappe di Karnaugh relative a z, y1*, y2* ed y3* sono:

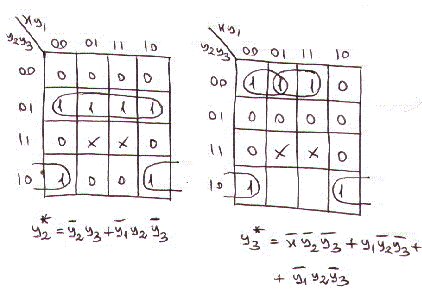
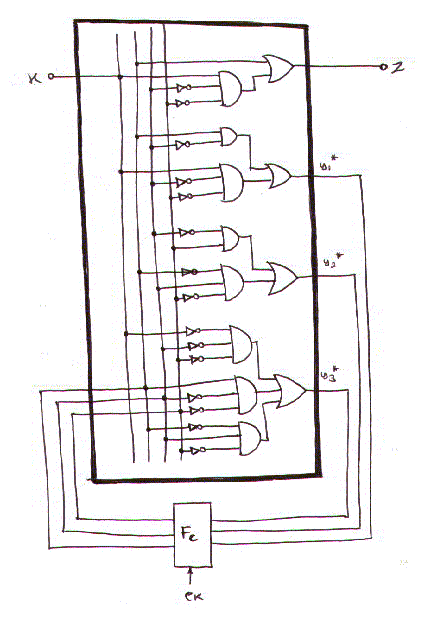
Infine la rete sequenziale che realizza il nostro automa e' la seguente: