Dunque per poter sintetizzare tale rete bisogna anzitutto cercare di risolvere il problema della chiusura della sbarra. Infatti se creo semplicemente una rete sequenziale che gestisca il parcheggio e chiuda la sbarra non appena la 2° macchina entra nel garage, rischio di far tagliare il veicolo in due!!!! Quindi e' necessario prima creare delle fotocellule intelligenti che non solo mi dicano che e' passato un automezzo, ma anche che me lo dicano proprio quando e' entrato del tutto (e non rischio cosi' incidenti di alcun tipo!)

Quindi progettiamo questa fotocellula "intelligente"

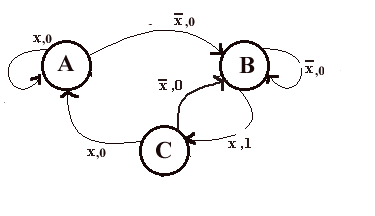
abbiamo 3 stati:

A - Non e' passata nessuna macchina
B - Sta passando una macchina
C - La macchina e' passata

chiamiamo X il segnale fornito dalla fotocellula quando non passa nulla e il segnale della fotocellula quando sta passando qualcosa. Come uscita in Z avremo 0 prima e durante l'attraversamento della vettura, mentre avremo 1 quando la vettura sara' passata del tutto dalla fotocellula

Codificheremo A con 01, B con 00 e C con 11, con tale codifica faremo coincidere Y'1 con Z ...ottenendo una notevole semplificazione nel circuito

Le mappe di Carnaugh che ne derivano saranno:

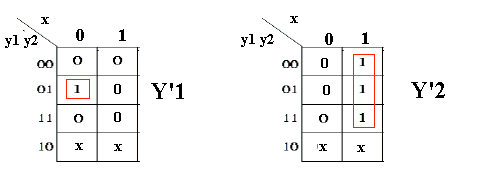
Dunque Y'1= y2 y1 x         e Y'2= x

Lo schema della fotocellula sara' dunque:

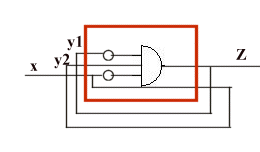
Ora si deve solo progettare il garage, gli stati interni sono:

A - Il garage e' vuoto
B - E' stata parcheggiata una macchina
C - Ci sono 2 macchine dentro

chiamo le 2 fotocellule F1 F2, la fotocellula segnata sara' quella che dara' il segnale di 1 (avvisando cioe' che una macchina e' appena entrata o appena uscita). Avremo il seguente diagramma degli stati (omettendo certi casi particolari che studieremo in seguito!!!!)

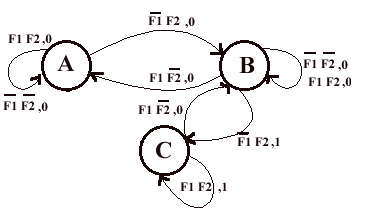
Tabella di flusso:

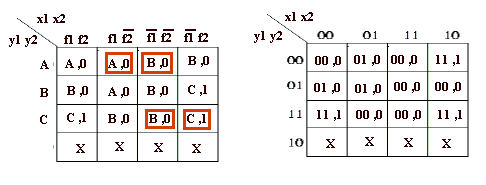
A=00, B=01 ,C=11

I casi in rosso sono casi eccezione, infatti se sono allo stato A, per esempio, e mi viene un segnale dalla fotocellula 2 (quella dell'uscita) non significhera' certo che e' uscita una macchina (il garage e' vuoto!) quindi deve essere passato un animale o una persona davanti alla fotocellula ... stato di nulla di fatto. Sempre considerando lo stato A, se arrivano segnali da entrambe le fotocellule, considero l'accensione della prima come input che e' entrata una macchina e l'input della 2°fotocellula come il passaggio di un pedone o qualcos'altro, ma non una vettura (a meno che lo spazio tra le 2 fotocellule non sia minore della lunghezza media di una macchina !!!) ... quindi passero' allo stato B! Stesso discorso per gli altri casi sottolineati in rosso!

Scriviamo ora le mappe di Carnaugh, al solito sono sufficienti solo quelli di Y1 e Y2 perche' Z e' identico a Y1

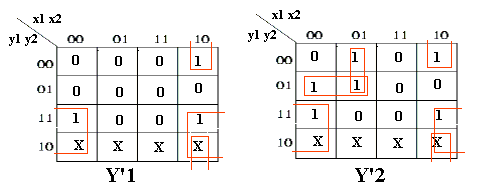
Y'1= Y1 X2 +  X1 X2 Y2                 Y'2=  Y1 X2 +  X1 X2 Y2 + Y1 Y2 X1 + Y1 X2 X1

Passiamo ora a disegnare il circuito sequenziale sfruttando queste espressioni algebriche.

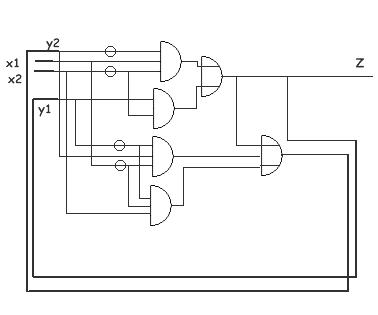
Purtroppo dopo aver fatto l'esercizio mi sono accorto dell'inutilita' dello stato interno C nella fotocellula "intelligente", questo avrebbe semplificato ulteriormente la sua realizzazione ...

Marco Salfi