Descriviamo l'automa a stati finiti che realizza la funzionalita' descritta nell'esercizio.
Gli interruttori di scaldabagno e lavatrice saranno connessi agli ingressi del nostro automa, dal quale, in uscita, verranno inviati i reali segnali di accensione.
L'insieme degli stati di ingresso sara' formato da coppie di informazioni yz che indicano se gli interruttori dello scaldabagno (y) o della lavatrice (z) sono stati premuti (1) o meno (0).
Stati di ingresso : {00,01,10,11}
L'insieme degli stati di uscita sara' formato da coppie di informazioni yz che indicano un segnale di accensione verso lo scaldabagno o la lavatrice.
Stati di uscita : {00,01,10,11}
Dall'analisi del problema si vede che gli stati interni in cui puo' trovarsi l'automa sono i seguenti:
- gli elettrodomestici sono entrambi spenti
- la lavatrice e' in funzione
- lo scaldabagno e' in funzione
Possiamo rappresentare questi stati interni, rispettivamente, con i simboli TS (Tutto Spento), LA (Lavatrice Accesa), SA (Scaldabagno Acceso).
Il diagramma degli stati sara' il seguente:

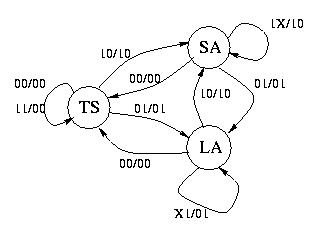
La tabella delle di flusso e' quindi

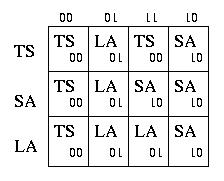
Non c'e' bisogno di fornire codifica per gli ingressi e le uscite.
Possiamo codificare gli stati interni con due bit nel modo seguente:
TS=00
SA=01
LA=11
La tabella delle transizioni sara' cosi'

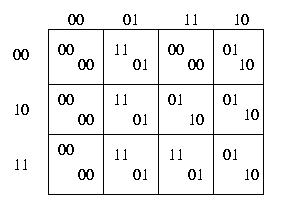
Indicando con x1 e x2 i bit in ingresso, con y1 e y2 i bit che codificano gli stati interni e con z1 e z2 i bit in uscita, possiamo ora dare le mappe di Carnaugh che descrivono le funzioni booleane per i bit di uscita e quelli che codificano gli stati interni successivi.

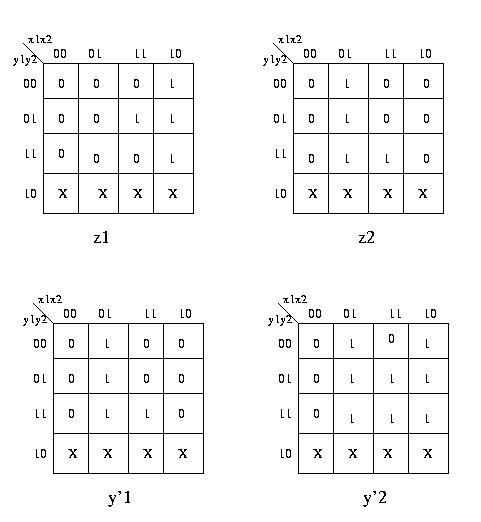
Vediamo subito che z2=y'1.
Cerchiamo ora di sintetizzare i circuiti minimali SP per le funzioni booleane descritte.

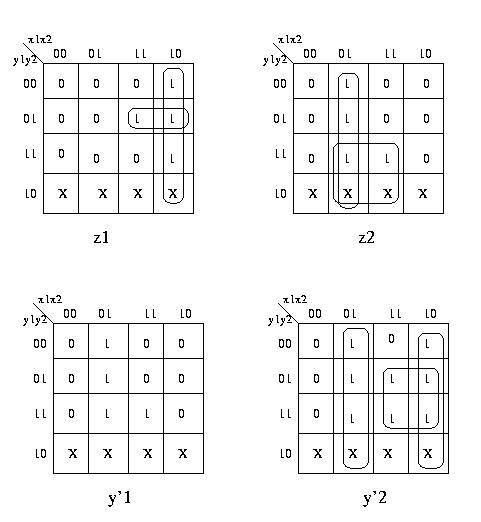
Le espressioni algebriche minimali sono quindi:
z1 = x1not(x2) + x1not(y1)y2
z2 = y'1 = not(x1)x2 + y1x2
y'2 = not(x1)x2 + x1not(x2) + x1y2

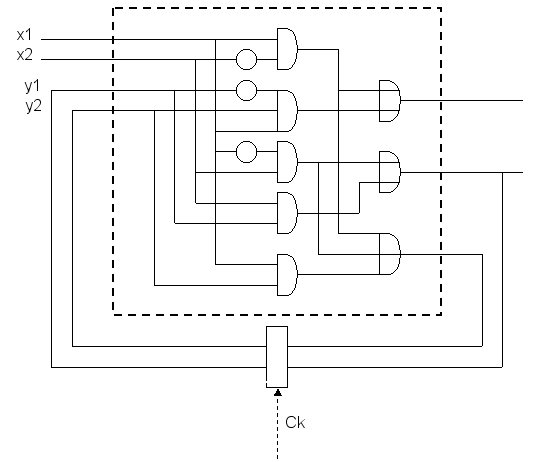
Possiamo ora disegnare il circuito sequenziale a partire da queste espressioni algebriche (By Claudio Bulla).

A questo punto qualcuno potrebbe essersi accorto di una possibilita' che potrebbe ridurre la complessita' del circuito.
Infatti, notate come, con la seguente codifica degli stati interni, differente da quella utilizzata,
TS=00
SA=10
LA=01
i segnali di uscita coincidono con quelli che codificano lo stato interno successivo. Questo permette nel nostro caso un circuito piu' semplice.
Come esercizio ulteriore, per chi non l'avesse gia' fatto, ripartire dalla tabella di flusso con la nuova codifica degli stati interni e rifare tutti i vari passi di sintesi.