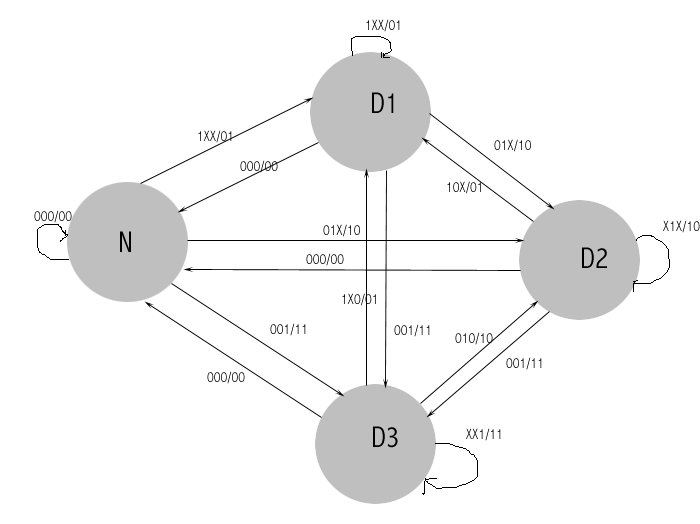
Lo stato N è lo stato in cui il bus è inutilizzato, mentre gli stati DX sono gli stati in cui il corrispondente stato X utilizza il bus. La corrispondente tabella di flusso è:
R1: request device 1
R2: request device 2
R3: request device 3
Mentre le uscite, che andranno a pilotare un multiplexer, e che attraverso un decoder fungeranno anche da linee di grant, saranno così:
00: nessuna richiesta per il bus
01: device 1 usa il bus
10: device 2 usa il bus
11: device 3 usa il bus
Vediamo ora lo schema del nostro automa:

Lo stato N è lo stato in cui il bus è inutilizzato, mentre
gli stati DX sono gli stati in cui il corrispondente stato X utilizza
il bus. La corrispondente tabella di flusso è:
| Stati\Input | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| N | 00/N | 11/D3 | 10/D2 | 10/D2 | 01/D1 | 01/D1 | 01/D1 | 01/D1 |
| D1 | 00/N | 11/D3 | 10/D2 | 10/D2 | 01/D1 | 01/D1 | 01/D1 | 01/D1 |
| D2 | 00/N | 11/D3 | 10/D2 | 10/D2 | 01/D1 | 01/D1 | 10/D2 | 10/D2 |
| D3 | 00/N | 11/D3 | 10/D2 | 11/D3 | 01/D1 | 11/D3 | 01/D1 | 11/D3 |
N=00
D1=01
D2=10
D3=11
Avrò che la codifica dello stato è uguale alla corrispondente
uscita, e quindi dovrò sviluppare solo le mappe per le due uscite,
invece di quattro per le uscite e gli stati. Abbiamo così la tabella
delle transizioni:
| Stati/Input | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 00 | 00 | 11 | 10 | 10 | 01 | 01 | 01 | 01 |
| 01 | 00 | 11 | 10 | 10 | 01 | 01 | 01 | 01 |
| 10 | 00 | 11 | 10 | 10 | 01 | 01 | 10 | 10 |
| 11 | 00 | 11 | 10 | 11 | 01 | 11 | 01 | 11 |
Le mappe di Karnaugh saranno:
R3=0
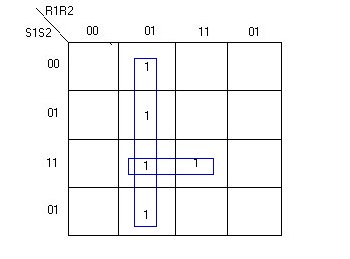
R3=1
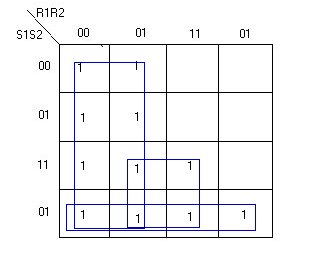
Ed otteniamo così:
U1=S1='R1R2'R3+R2S1S2'R3+'R1R3+R2S2R3+S1'S2R3
Mentre per l'altra uscita avremo:
R3=0
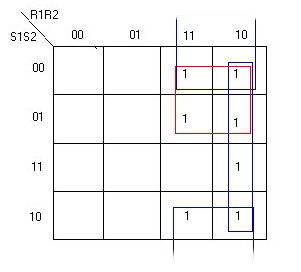
R3=1
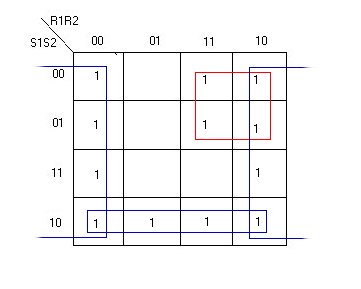
Ed otterremo:
U2=S2=R1'S1+R1'S2'R3+R1'R2'R3+'R2R3+S1'S2R3
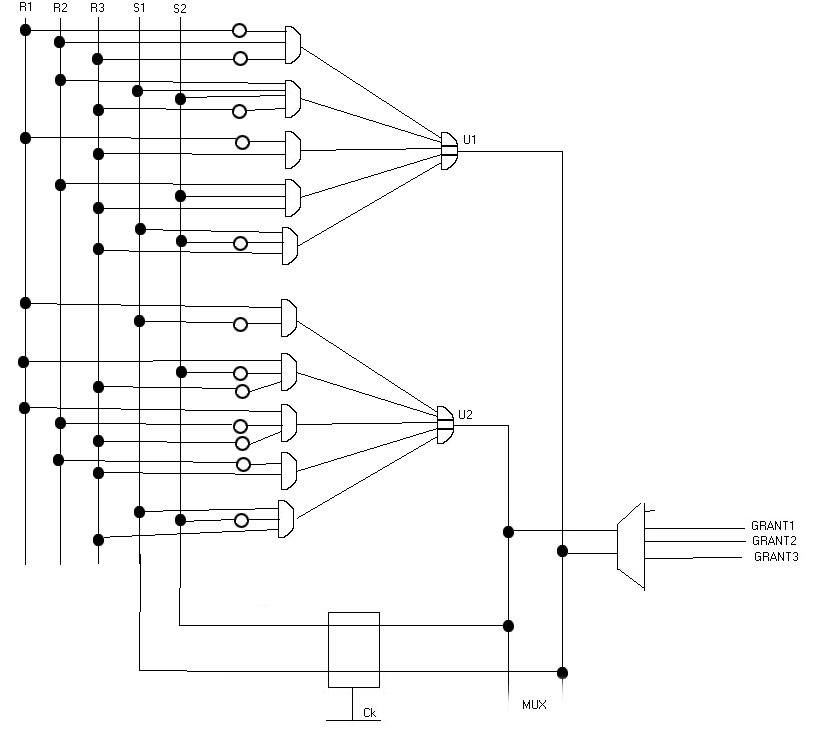
Otteniamo infine lo schema: