DMI – Corso di laurea in Informatica
Copyleft
![]() 2019 Giuseppe Scollo
2019 Giuseppe Scollo
precursori della formalizzazione logica: da Aristotele a Leibniz
Leibniz anticipa di un paio di secoli l'intuizione di George Boole: le leggi di un'algebra del pensiero
in prima approssimazione: un insieme + operazioni su di esso
le equazioni giocano un ruolo fondamentale nell'algebra tradizionale:
sono non meno fondamentali nell'algebra astratta (XX secolo), dove però:
il concetto di algebra, nella prima approssimazione introdotta sopra, si generalizza a quello di struttura algebrica, in cui si distingue:
una ridotta di una struttura A è una struttura costituita da un sottoinsieme delle operazioni e relazioni di A, definite sullo stesso sostegno
una struttura si dice omogenea se il sostegno consta di un solo insieme
una struttura dotata solo di operazioni totali è detta algebra in senso stretto
N.B.: è sempre possibile rappresentare una struttura algebrica come
semigruppo :
(A ; ⋅), con ⋅
un'operazione binaria associativa
monoide :
(A ; e,⋅),
un semigruppo
(A ; ⋅)
con e costante
neutra rispetto
a ⋅
gruppo [commutativo]:
(A ; e,⋅,— ),
un monoide [commutativo]
(A ; e,⋅)
con un'operazione unaria —
che dà l'inverso rispetto a
⋅
ed e :
⋅—x
= —x⋅x
= e
semianello [commutativo]:
(A ; 0, 1, +, ⋅),
un monoide commutativo
(A ; 0, +), detto additivo,
e un monoide [commutativo]
(A ; 1,⋅), detto
moltiplicativo, tali da soddisfare:
⋅(y+z)
=
(x⋅y)+(x⋅z),
(x+y)⋅z
=
(x⋅z)+(y⋅z)
⋅ x
=
x ⋅ 0
= 0
anello [commutativo]:
(A ; 0, 1, +, ⋅,—),
un semianello [commutativo]
(A ; 0, 1, +, ⋅), con il monoide additivo esteso a un gruppo commutativo
(A ; 0, +, —)
classi di algebre in senso stretto quali quelle viste in precedenza sono caratterizzate da assiomi di forma molto semplice:
= t2 (con implicita quantificazione universale)
quando una classe di algebre è caratterizzata da un insieme di equazioni, che ne costituisce la base assiomatica, è possibile dedurre da tale base tutte le equazioni valide in ogni algebra della classe mediante le regole del calcolo equazionale di Garrett Birkhoff:
⊢
t = t
= t2
⊢ t2
= t1
= t2,
t2
= t3
⊢ t1
= t3
= t2
⊢
τ(t1)
=
τ(t2)
= t2
⊢
t
[u ← t1]
=
t
[u ← t2]
← t ' ]
è ottenuto dal termine t rimpiazzando il suo sottotermine al posto
u con il termine t '
un reticolo è un ordinamento parziale in cui ogni coppia di elementi abbia:
alternativamente, per via strettamente algebrica:
⋅
è espressa dall'equazione x⋅x = x)
∨,∧)
tale che le sue due ridotte
(A; ∨),
(A; ∧)
sono semireticoli, e inoltre valgono gli assiomi di assorbimento:
∨
(x ∧
y) = x
x ∧
(x ∨
y) = x
occorrono dunque 8 equazioni per la base assiomatica dei reticoli?
che fine ha fatto l'ordinamento del reticolo? lo si può definire algebricamente come abbreviazione di equazioni (equivalenti) in ciascuna delle due operazioni binarie:
≤
y
≡
x
∨
y
=
y
oppure:
x
≤
y
≡
x
∧
y
=
x
un reticolo è completo se ogni insieme di suoi elementi ha minimo maggiorante e massimo minorante
un reticolo è detto distributivo se ciascuna delle sue due operazioni è distributiva rispetto all'altra
caratterizzazione M3-N5 dei reticoli non distributivi:
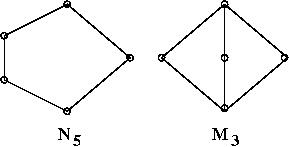
un reticolo è detto limitato se ha un massimo 1 e un minimo 0
un reticolo limitato è detto complementato
se ammette un'operazione unaria di complemento
- tale da soddisfare:
x
∨
-x
= 1
e:
x
∧
-x
= 0
un'algebra di Boole (o booleana) è un reticolo distributivo complementato
mettendo assieme le equazioni che caratterizzano i reticoli distributivi complementati, si ottiene una base assiomatica di 12 equazioni per le algebre di Boole
un paio di domande si sono presto imposte all'attenzione:
alla risposta (negativa) alla prima domanda è seguita la ricerca di una risposta alla seconda:
—) così
ridotte, dovuta a E.V. Huntington (1933), consta di solo 3 equazioni:
associatività e commutatività di + e assioma di Huntington:
—(—x + y)
+ —(—x +
—y)
= x
su qualsiasi insieme S possono costruirsi algebre booleane di insiemi, ciascuna così fatta:
si verifica che l'ordinamento booleano è l'inclusione di insiemi nella famiglia
Teorema di rappresentazione di Stone:
qualsiasi sistema di assiomi completo per le algebre di Boole fornisce
un calcolo deduttivo completo per la logica
proposizionale:
⊢ φ = 1
sse ⊨ φ
= ψ sse
⊨ φ ↔ ψ
sse
φ, ψ logicamente equivalenti
possiamo costruire un'algebra booleana delle formule proposizionali, dove si identifichino formule equivalenti? (semantica algebrica della logica proposizionale)
l'algebra di Lindenbaum-Tarski è una tal costruzione; fissato un insieme V di variabili proposizionali:
si veda l'esercizio sulla definizione dell'algebra di Lindenbaum-Tarski
di particolare interesse per la realizzazione di macchine da calcolo fisiche è l'algebra booleana minimale, o algebra binaria di commutazione (Switching Algebra), caratterizzata dal fatto che il sostegno consta solo delle due costanti booleane (distinte)
l'algebra booleana minimale è isomorfa all'algebra di Lindenbaum‑Tarski generata dall'insieme vuoto di variabili
l'algebra booleana minimale offre un'interpretazione dei simboli di costante come valori di verità e degli operatori booleani come connettivi proposizionali
i due operatori
(∨,—)
sono sufficienti a definire qualsiasi funzione booleana, cioè funzione n-aria su {0,1}
∧
con una legge di De Morgan
Un insieme di operatori booleani si dice funzionalmente completo se ogni funzione booleana è rappresentabile da un termine contenente solo variabili e operatori nell'insieme
∧,—),
e i singoli
∨ e
∧
si possono definire funzioni numeriche finite mediante funzioni booleane grazie alla rappresentazione binaria dei numeri (già intuita da Leibniz)
sono detti porte logiche (gate) componenti fisici con vie di ingresso e di uscita che esibiscano il comportamento di ingresso/uscita proprio di operatori booleani
si realizzano in tal modo circuiti logici, classificabili in due categorie:
in una rete combinatoria l'output a un dato istante dipende solo dai valori in input a quell'istante, mentre in un circuito sequenziale si ha la dipendenza dell'output dalla precedente sequenza temporale degli input